某餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）当有
张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？
某蛋糕产销公司A品牌产销线，2015年的销售量为9.5万份，平均每份获利1.9元，预计以后四年每年销售量按5000份递减，平均每份获利按一定百分数逐年递减；受供给侧改革的启发，公司早在2014年底就投入资金10.89万元，新增一条B品牌产销线，以满足市场对蛋糕的多元需求，B品牌产销线2015年的销售量为1.8万份，平均每份获利3元，预计以后四年销售量按相同的份数递增，且平均每份获利按上述递减百分数的2倍逐年递增；这样，2016年，A、B两品牌产销线销售量总和将达到11.4万份，B品牌产销线2017年销售获利恰好等于当初的投入资金数．
（1）求A品牌产销线2018年的销售量；
（2）求B品牌产销线2016年平均每份获利增长的百分数．
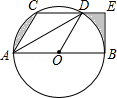
如图，CD是⊙O的弦，AB是直径，且 ，连接AC、AD、OD，其中 ，过点B的切线交CD的延长线于E．
（1）求证：DA平分∠CDO；
（2）若AB＝12，求图中阴影部分的周长之和（参考数据： ， ）．
某小学学生较多，为了便于学生尽快就餐，师生约定：早餐一人一份，一份两样，一样一个，食堂师傅在窗口随机发放（发放的食品价格一样），食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品．
（1）按约定，“小李同学在该天早餐得到两个油饼”是 事件；（可能，必然，不可能）
（2）请用列表或树状图的方法，求出小张同学该天早餐刚好得到猪肉包和油饼的概率．
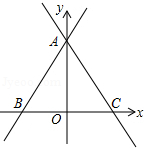
如图，直线 与两坐标轴分别交于A、B两点．
（1）求∠ABO的度数；
（2）过A的直线l交x轴正半轴于C， ，求直线l的函数解析式．
杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：
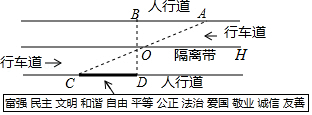
如图， ，相邻两平行线间的距离相等，AC，BD相交于O， ．垂足为D，已知 米，请根据上述信息求标语CD的长度．