出租车司机小石某天下午营运全是在东西走向的人民大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-3,+14,-11,+10,-12.
(1)将最后一名乘客送达目的地时,小石距下午出发地点的距离是多少千米?
(2)若汽车耗油量为0.3升/千米,这天下午汽车耗油共多少升?
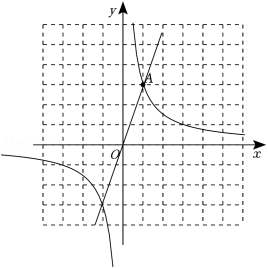
已知:点 是反比例函数 的图象与直线 的一个交点.
(1)求 的值;
(2)在第一象限内,当 时,请直接写出 的取值范围.
解不等式 ,并把解集在数轴上表示出来.
如图,抛物线 ( 是常数)的顶点为 ,与 轴交于 两点, ,点 为线段 上的动点,过 作 交 于点 .
(1)求该抛物线的解析式;
(2)求 面积的最大值,并求此时 点坐标.

如图,四边形 内接于 , 为 的直径, .
(1)试判断 的形状,并给出证明;
(2)若 , ,求 的长度.

为振兴乡村经济,在农产品网络销售中实行目标管理,根据目标完成的情况对销售员给予适当的奖励,某村委会统计了 名销售员在某月的销售额(单位:万元),数据如下:
(1)补全月销售额数据的条形统计图.

(2)月销售额在哪个值的人数最多(众数)?中间的月销售额(中位数)是多少?平均月销售额(平均数)是多少?
(3)根据(2)中的结果,确定一个较高的销售目标给予奖励,你认为月销额定为多少合适?