如图,在平面直角坐标系中,直线l:y=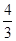 x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.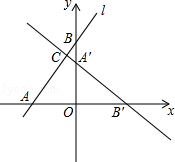
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线l相交于点C,求△A′BC的面积.
如图,P是⊙O的直径AB延长线上的一点, PC切⊙O于点C,弦CD⊥AB,垂足为点E,若 ,
,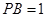 .
.
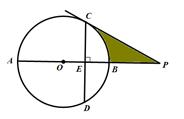
求:(1)⊙O的半径;
(2)CD的长;
(3)图中阴影部分的面积.
已知:抛物线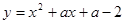 .
.
(1)求证:不论a取何值时,抛物线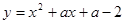 与x轴都有两个不同的交点.
与x轴都有两个不同的交点.
(2)设这个二次函数的图象与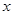 轴相交于A(
轴相交于A(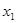 ,0),B(
,0),B(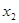 ,0),且
,0),且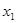 、
、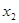 的平方和为3,求a的值.
的平方和为3,求a的值.
已知二次函数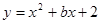 的图像经过点(-1,6)
的图像经过点(-1,6)
(1)求这个二次函数的关系式;
(2)求二次函数图像与x轴的交点的坐标;
(3)画出图像的草图,观察图像,直接写出当y>0时,x的取值范围.
分别求出对应的二次函数的解析式:
(1)已知抛物线的顶点为(-2,1),且过点(-4,3);
(2)抛物线与x轴的两个交点坐标为(-3,0)和(2,0),且它经过点(1,4).
如图, ΔABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F。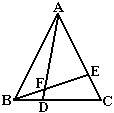
(1)求证:ΔABD≌ΔBCE.
(2)ΔAEF与ΔABE相似吗?请说明理由.
(3)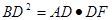 成立吗?请说明理由.
成立吗?请说明理由.