如图，在四边形ABCD中，AB⊥BC，CD⊥BC，AB=2，BC=CD=4，AC、BD交于点O，在线段BC上，动点M以每秒1个单位长度的速度从点C出发向点B做匀速运动，同时动点N从点B出发向点C做匀速运动，当点M、N其中一点停止运动时，另一点也停止运动，分别过点M、N做BC的垂线，分别交AC、BD于点E、F，连接EF．若运动时间为x秒，在运动过程中四边形EMNF总为矩形（点M、N重合除外）．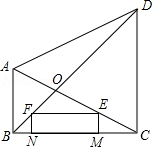
（1）求点N的运动速度；
（2）当x为多少时，矩形EMNF为正方形？
（3）当x为多少时，矩形EMNF的面积S最大？并求出最大值．
，其中
。
的值
