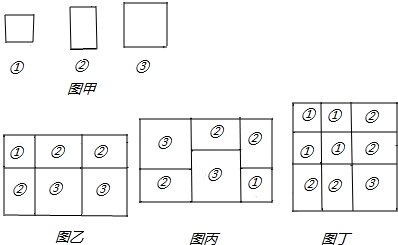
为了解某校七、八年级学生的睡眠情况,随机抽取了该校七、八年级学生部分学生进行调查.已知抽取七年级与八年级的学生人数相同,且八年级学生的D组有15人,利用抽样所得的数据绘制所示的统计图表.
睡眠情况分组表(单位:时)
| 组别 |
睡眠时间x |
| A |
x≤7.5 |
| B |
7.5≤x≤8.5 |
| C |
8.5≤x≤9.5 |
| D |
9.5≤x≤10.5 |
| E |
x≥10.5 |
根据图表提供的信息,回答下列问题:
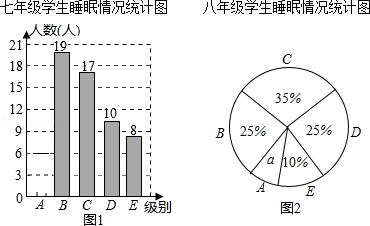
(1)此次调查抽取样本容量是 ;七年级学生睡眠时间在A组的有 人;并补全七年级学生睡眠情况统计图;
(2)求“八年级学生睡眠情况统计图”中的a及a对应的扇形的圆心角度数;
(3)抽取的样本中七、八年级学生睡眠时间在C组的共有多少人?
(4)已知该校七年级学生有800人,八年级学生有850人,如果睡眠时间x(时)满足:7.5≤x≤9.5,称睡眠时间合格,试估计该校七、八年级学生睡眠时间合格的共有多少人?
如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,
求证:△ABD≌△AEC.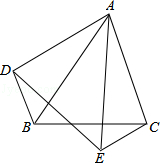
如图(图略),从一副扑克牌中选取红桃10,方块10,梅花5,黑桃8四张扑克牌,洗匀后正面朝下放在桌子上,甲先从中任意抽取一张后,乙再从剩余的三张扑克牌中任意抽取一张,用画树形图或列表的方法,求甲乙两人抽取的扑克牌的点数都是10的概率.
为促进交于均能发展,A市实行“阳光分班”,某校七年级一班共有新生45人,其中男生比女生多3人,求该班男生、女生各有多少人.
先化简,再求值:x(x+3)﹣(x+1)2,其中x=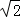 +1.
+1.
阅读材料并解决问题:
我们已经知道完全平方公式可以用平面几何图形拼图来表示面积,实际上还有一些多项式乘法也可以用这种拼图形式来表示结果,例如:(a+2b)(a+b)=a2+3ab+2b2就可以用图甲中的①、②、③表示图乙或图丙图形的面积.
(1)请你写出图丁所表示的整式乘法及其结果;
(2)画出一个几何图形,使它的面积能表示:(a+2b)(a+b)=a2+3ab+2b2【注意要在图中标出①②③】
(3)请仿照上述方法另写一个含有a、b的整式乘法及其结果,并画出与之相应的几何图形.