在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.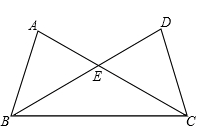
(1)求证:△ABE≌DCE;
(2)当∠AEB=50°,求∠EBC的度数?
先化简代数式 ,求:当a=2时代数式值.
,求:当a=2时代数式值.
已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b﹣3)2=0,
(1)则a= ,b= ;并将这两数在数轴上所对应的点A、B表示出来;
(2)数轴上在B点右边有一点C到A、B两点的距离和为11,求点C在数轴上所对应的数;
(3)若A点,B点同时沿数轴向正方向运动.点A的速度是点B的2倍,且3秒后,2OA=OB,求点B的速度.
友情提示:M、N之间距离记作 ,点M、N在数轴上对应的数分别为m、n,则
,点M、N在数轴上对应的数分别为m、n,则 .
.
一列火车匀速行驶,经过一条长300米的隧道需要20s的时间,隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10s.
(1)设火车的长为xm,用含x的式子表示:从火车头经过灯下到车尾经过灯下火车所走的路程是______;这段时间火车的平均速度是________;
(2)求这列火车的长度.
列方程解应用题:
(1)某车间32名工人生产螺母和螺钉,每人每天平均生产螺钉1500个或螺母5000个,一个螺钉要配两个螺母,为了使每天的产品刚好配套,应该分配多少名工人生产螺钉?
(2)一艘船从甲码头到乙码头顺流行驶用4小时,从乙码头到甲码头逆流行驶用4小时40分钟,已知水流速度为3千米/小时,则船在静水中的平均速度是多少?