平面内的两条直线有相交和平行两种位置关系
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
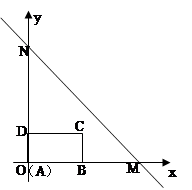
如图,直线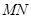 :
: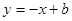 与
与 轴交于点
轴交于点 (4,0),与
(4,0),与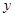 轴交于点
轴交于点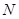 ,长方形
,长方形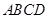 的边
的边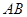 在
在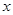 轴上,
轴上,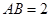 ,
,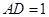 .长方形
.长方形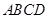 由点
由点 与点
与点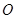 重合的位置开始,以每秒1个单位长度的速度沿
重合的位置开始,以每秒1个单位长度的速度沿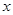 轴正方向作匀速直线运动,当点
轴正方向作匀速直线运动,当点 与点
与点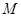 重合时停止运动.设长方形运动的时间为
重合时停止运动.设长方形运动的时间为 秒,长方形
秒,长方形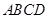 与△
与△ 重合部分的面积为
重合部分的面积为 .
.
(1)求直线 的解析式;
的解析式;
(2)当 =1时,请判断点
=1时,请判断点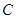 是否在直线
是否在直线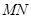 上,并说明理由;
上,并说明理由;
(3)请求出当 为何值时,点
为何值时,点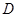 在直线
在直线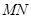 上;
上;
(4)直接写出在整个运动过程中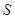 与
与 的函数关系式.
的函数关系式.
已知:在△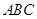 中,
中,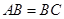 ,
,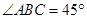 ,
,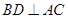 于
于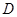 ,
,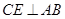 于点
于点 ,
, 、
、 相交于
相交于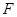 .
.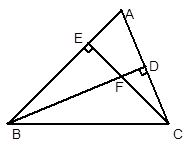
(1)求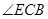 的度数;
的度数;
(2)求证:△ ≌△
≌△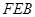 ;
;
(3)探究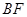 与
与 的数量关系,并给予证明.
的数量关系,并给予证明.
某市医药公司的甲、乙两仓库分别存有某种药品80箱和70箱,现需要将库存的药品调往A地100箱和B地50箱.
(1)设从甲仓库运送到A地的药品为 箱,请填写下表:
箱,请填写下表:
 |
甲仓库 |
乙仓库 |
总计 |
 地 地 |
 箱 箱 |
①箱 |
100箱 |
 地 地 |
②箱 |
③箱 |
50箱 |
| 总计 |
80箱 |
70箱 |
150箱 |
(2)已知从甲、乙两仓库运送药品到两地的费用(元/箱)如右表所示.求总费用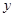 (元)与
(元)与 (箱)之间的函数关系式,并写出
(箱)之间的函数关系式,并写出 的取值范围;
的取值范围;
(3)求出最低总费用,并说明总费用最低时的调配方案.
| 地名 |
费用(元/箱) |
|
| 甲库 |
乙库 |
|
| A地 |
14 |
20 |
| B地 |
10 |
8 |
(1)作出△ABC关于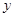 轴对称的△A1B1C1,并写出△A1B1C1中顶点C1的坐标;
轴对称的△A1B1C1,并写出△A1B1C1中顶点C1的坐标;
(2)将△ABC向右平移6个单位长度,作出平移后的△A2B2C2,并写出△A2B2C2中顶点C2的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴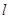 .
. 
如图,点B、D、C、F在一条直线上,且BD=FC,AB=EF.
(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添加的条件是 ;
(2)添加了条件后,证明△ABC≌△EFD.