果农老张进行桃树科学管理试验．把一片桃树林分成甲、乙两部分，甲地块用新技术管理，乙地块用老方法管理，管理成本相同．在甲、乙两地块上各随机选取40棵桃树，根据每棵树的产量把桃树划分成A，B，C，D，E五个等级（甲、乙两地块的桃树等级划分标准相同，每组数据包括左端点不包括右端点）．画出统计图如下：
（1）补齐直方图，求a的值及相应扇形的圆心角度数；
（2）选择合适的统计量，比较甲乙两地块的产量水平．并说明试验结果；
（3）若在甲地块随机抽查1棵桃树，求该桃树产量等级是B级的概率．
如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP．
⑴如图②，若M为AD边的中点，①△AEM的周长=_____cm；②求证：EP=AE+DP；
⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．
（本题13分）当Rt⊿的直角顶点P要正方形ABCD对角线AC上运动（P与A、C不重合）且一直角边始终过点D，另一直角边与射线BC交于点E，
（1）如图1，当点E与BC边相交时，
①证明：⊿PBE为等腰三角形；
②写出线段AP、PC与EC之间的等量关系(不必证明)
（2）当点E在BC的延长线上时,请完成图2,并判断(1)中的①、②结论是否分别成立？若不成立，写出相应的结论(不必证明)
（12′）王华、张伟两位同学九年级10次数学单元自我检测的成绩（成绩均为整数，且个位数为0）分别如下图所示：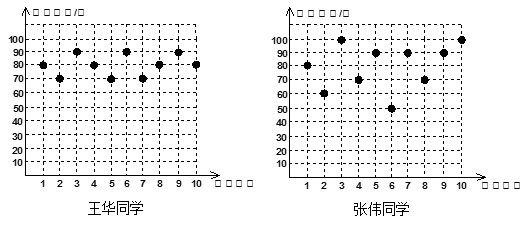
（1）根据上图中提供的数据填写下表：
| 平均成绩 |
中位数 |
众数 |
方差（S2） |
|
| 王华 |
80 |
|||
| 张伟 |
85 |
260 |
（2）如果将90分以上（含90分）的成绩视为优秀，则优秀率高的同学是________.
（3）如果要从这两个同学选一位去参加数学竞赛，你可以给老师一些建议吗？
如图，矩形ABCD中，对角线AC、BD交于点O，DE∥OC，CE∥OD，试判断四边形OCDE是何特殊四边形，并加以证明。（8′）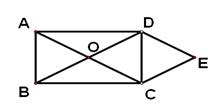
先将
化简，然后选取一个你喜欢的a的值，代入求值．