如图1,P(m,n)是抛物线y=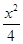 -1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
-1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
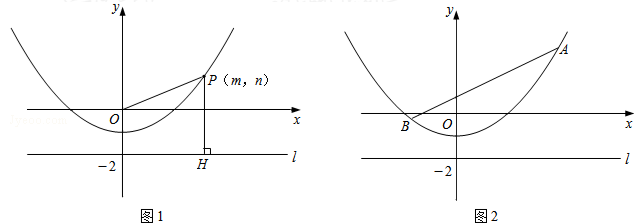
【探究】
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= ;
【证明】
(2)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
【应用】
(3)如图2,已知线段AB=6,端点A,B在抛物线y=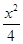 -1上滑动,求A,B两点到直线l的距离之和的最小值.
-1上滑动,求A,B两点到直线l的距离之和的最小值.
某精品水果超市销售一种进口水果A,从去年1至7月,这种水果的进价一路攀升,每千克A的进价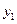 与月份
与月份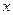 (
(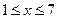 ,且
,且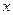 为整数),之间的函数关系式如下表 :
为整数),之间的函数关系式如下表 :
月份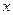 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
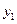 (元/千克) (元/千克) |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
随着我国对一些国家进出口关税的调整,该水果的进价涨势趋缓,在8至12月份每千克水果A的进价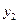 与月份
与月份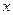 (
(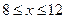 ,且
,且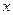 为整数)之间存在如下图所示的变化趋势.
为整数)之间存在如下图所示的变化趋势.
(1)请观察表格和图像,用所学过的一次函数、反比例函数、二次函数的有关知识分别写出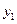 与
与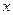 和
和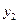 与
与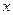 的函数关系式.
的函数关系式.
(2)若去年该水果的售价为每千克180元,且销售该水果每月必须支出(除进价外)的固定支出为300元,已知该水果在1月至7月的销量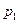 (千克)与月份
(千克)与月份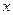 满足:
满足: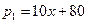 ;8月至12月的销量
;8月至12月的销量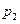 (千克)与月份
(千克)与月份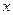 满足:
满足: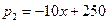 ;则该水果在第几月销售时,可使该月所获得的利润最大?并求出此时的最大利润.
;则该水果在第几月销售时,可使该月所获得的利润最大?并求出此时的最大利润.
(3)今年1月到6月,该进口水果的进价进行调整,每月进价均比去年12月的进价上涨15元,且每月的固定支出(除进价外)增加了15%,已知该进口水果的售价在去年的基础上提高了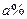 (
(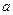 <100),与此同时每月的销量均在去年12月的基础上减少了
<100),与此同时每月的销量均在去年12月的基础上减少了 ,这样销售下去要使今年1至6月的总利润为68130元,试求出
,这样销售下去要使今年1至6月的总利润为68130元,试求出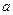 的值.(保留两个有效数字)(参考数据:
的值.(保留两个有效数字)(参考数据: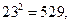
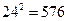 ,
,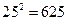 ,
,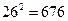 )
)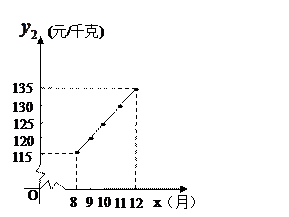
如图,在梯形ABCD中,AD∥BC,点E为CD上一点,且DE=EC=BC.
(1)若∠B=90°,求证: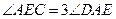 ;
;
(2)若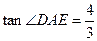 ,AD=2,AE=5,求梯形ABCD的面积.
,AD=2,AE=5,求梯形ABCD的面积.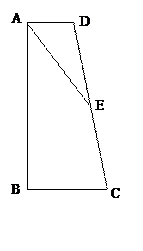
元旦晚会即将来临,小涵作为晚会主持人为本次晚会准备了A等,B等,C等,D等共
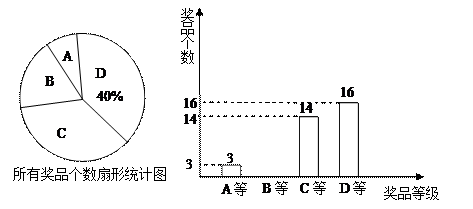
4类奖品,它们的价格可由下表表示 ,小涵绘制了如下两幅不完整的统计图:
 |
| 等级 |
价格(元/个) |
| A等 |
50 |
| B等 |
30 |
| C等 |
20 |
| D等 |
10 |
(1)小涵总共准备了__________个奖品,这些奖品平均每个的价格为__________元.
(2)补全条形统计图.
(3)在晚会的摸奖环节中,所有奖品均已发出,其中获得A等奖的有1位女同学,B等奖有4位女同学.现从获得A等和B等的同学中分别抽出一位做获奖感言,那么请你用画树状图或列表格的方法求出恰好有一位男同学和一位女同学做获奖感言的概率.
如图,在平面直角坐标系中,一次函数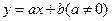 与x轴、
与x轴、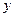 轴分别交于点C、
轴分别交于点C、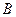 ,与反比例函数
,与反比例函数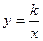 (k≠0)相交于A、D两点,其中BD=5,BO=2,
(k≠0)相交于A、D两点,其中BD=5,BO=2,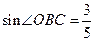 .
.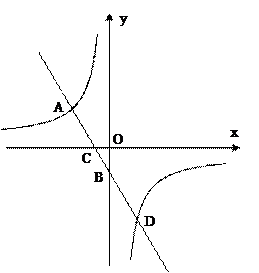
(1) 分别求出反比例函数和直线AB的解析式;
(2) 连接OD,求△COD的面积.
先化简,再求值: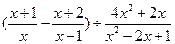 ,其中x满足方程
,其中x满足方程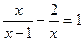 .
.