甲口袋中装有2个相同的小球，它们分别写有数值-1，5；乙口袋中装有3个相同的小球，它们分别写有数值-4，2，3．现从甲口袋中随机取一球，记它上面的数值为m，再从乙口袋中随机取一球，记它上面的数值为n．设点A的坐标为（m，n）．
（1）请用树状图或列表法，列出（m，n）所有可能的结果；
（2）求点A落在第一象限的概率．
解方程组
（1）
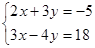（2）
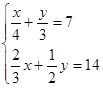
如图，△ABC中，点D在BC的延长线上，过D作DE⊥AB于E，交AC于F。已知∠A=30°，∠FCD=80°，求∠D的度数。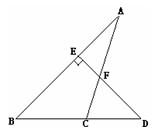
在图所示的平面直角坐标系中表示下面各点：。
A（0，3），B（1，－3），C（3，－5），D（－3，－5），E（3，5），F（5，7）。
（1）A点到原点O的距离是__ __个单位长。
（2）将点C向左平移6个单位，它会与点重合。
（3）连接CE，则直线CE与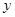
轴是什么位置关系？
（4）点F到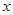
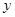、轴的距离分别是多少？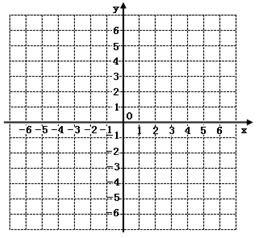
已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数。
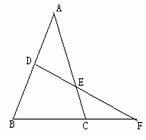
如图，直线DE交△ABC的边AB、AC于D、E，交BC的延长线于点F，若∠B＝67°，∠ACB＝74°，∠AED＝48°，求∠BDF的度数。