阅读以下材料:
对于三个数a、b、c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=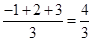 ;min{-1,2,3}=-1,…解决下列问题:
;min{-1,2,3}=-1,…解决下列问题:
(1)填空:如果min{2,2x+2,4-2x}=2,则x的取值范围为 ;
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论:如果M{a,b,c}=min{a,b,c},那么 (填a、b、c的大小关系),证明你发现的结论.
③运用②的结论,填空:若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,+2x-y,则x+y=
(3)在同一直角坐标系中作出函数y=x+1,y=(x-1)2,y=2-x的图象(不需列表描点),通过观察图象,填空:min{x+1,(x-1)2,2-x}的最大值为 .
(本题共2小题,每小题5分,满分10分)
已知:如图,BC是⊙O的弦,点A在⊙O上,AB =" AC" = 10,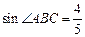 .
.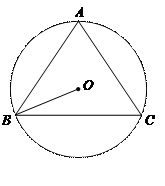
求:(1)弦BC的长;
(2)∠OBC的正切的值.
解不等式组: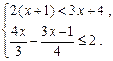 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.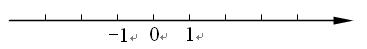
先化简,再求 值:
值: ,其中
,其中 .
.
(本题满分14分,第(1)小题满分6分,第(2)小题满分5分,第(3)小题
满分3分) 如图,在半径为5的⊙O中,点A、B在⊙O上,∠AOB=90º
如图,在半径为5的⊙O中,点A、B在⊙O上,∠AOB=90º ,点C是AB上的一个动点,AC与OB的延长线相交于点D,设AC=
,点C是AB上的一个动点,AC与OB的延长线相交于点D,设AC= ,BD=
,BD= .
.
(1)求 关于
关于 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(2)如果⊙ 与⊙O相交于点A、C,且⊙
与⊙O相交于点A、C,且⊙ 与⊙O的圆心距为2,当BD=
与⊙O的圆心距为2,当BD= OB时,求⊙
OB时,求⊙ 的半径;
的半径;
(3)是否存在点C,使得△DCB∽△DOC?如果存在,请证明; 如果不存在,请简要说明理由.
如果不存在,请简要说明理由.
(本题满分12分,第(1)小题满分3分,第(2)小题满分9分)
如图, 二次函数 的图像与
的图像与 轴
轴 、
、 轴的交点分别为A、B,点C在这个二次函数的图像上,且∠ABC=90º,∠CAB=∠BAO,
轴的交点分别为A、B,点C在这个二次函数的图像上,且∠ABC=90º,∠CAB=∠BAO, .
.
(1)求点A的坐标;
(2 )求这个二次函数的解析式.
)求这个二次函数的解析式.