某中学举行数学知识竞赛，所有参赛学生分别设有一、二、三等奖和纪念奖，获奖情况已绘制成如图所示的两幅不完整的统计图．根据图中所给出的信息解答下列问题：
（1）二等奖所占的比例是多少？
（2）这次数学知识竞赛获得二等奖的人数是多少？
（3）请将条形统计图补充完整；
（4）若给所有参赛学生每人发一张卡片，各自写上自己的名字，然后把卡片放入一个不透明的袋子里，摇匀后任意摸出一张，求摸出的卡片上是写有一等奖学生名字的概率．
如图，将▱ABCD的AD边延长至点E，使DE=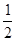
AD，连接CE，F是BC边的中点，连接FD．
（1）求证：四边形CEDF是平行四边形；
（2）若AB=3，AD=4，∠A=60°，求CE的长．
先化简，再求值：
，其中x=﹣3．
如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=5
，且
，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：y=－
+c经过点E，且与AB边相交于点F．
（1）求证：△ABD∽△ODE；
（2）若M是BE的中点，连接MF，求证：MF⊥BD；
（3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．
五边形ABCDE中，∠EAB=∠ABC=∠BCD=90°，AB=BC，且满足以点B为圆心，AB长为半径的圆弧AC与边DE相切于点F，连接BE，BD．
（1）如图1，求∠EBD的度数；
（2）如图2，连接AC，分别与BE，BD相交于点G，H，若AB=1，∠DBC=15°，求AG•HC的值．
阅读材料：善于思考的小军在解方程组
时，采用了一种“整体代换”的解法：
解：将方程②变形：4x+10y+y="5" 即2（2x+5y）+y=5③
把方程①带入③得：2×3+y=5，∴y=﹣1
把y=﹣1代入①得x=4，∴方程组的解为
．
请你解决以下问题：
（1）模仿小军的“整体代换”法解方程组
（2）已知x，y满足方程组
．
（i）求
的值；
（ii）求
的值．