如图①，在矩形ABCD中，AB=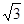
，BC=3，在BC边上取两点E、F（点E在点F的左边），以EF为边所作等边△PEF，顶点P恰好在AD上，直线PE、PF分别交直线AC于点G、H．
（1）求△PEF的边长；
（2）若△PEF的边EF在线段CB上移动，试猜想：PH与BE有何数量关系？并证明你猜想的结论；
（3）若△PEF的边EF在射线CB上移动（分别如图②和图③所示，CF＞1，P不与A重合），（2）中的结论还成立吗？若不成立，直接写出你发现的新结论．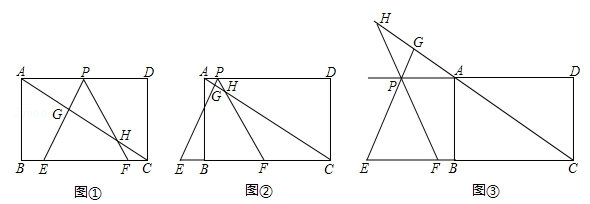
（本题8分）一列快车由甲地开往乙地，一列慢车由乙地开往甲地, 两车同时出发,沿同一条道路匀速行驶.设行驶时间为t（h），两车之间的距离为s（km），图中折线A-B-C-D表示s与t之间的函数关系.
（1）甲、乙两地相距km，两车出发后h相遇；
（2）通过计算说明，当快车到达乙地时，慢车还要多少时间才能到达甲地？
（本题8分）为提高初中生的身体素质，教育行政部门规定：初中生每天参加户外活动的平均时间应不少于1小时．为了解学生参加户外活动的情况，某县教育行政部门对部分学生参加户外活动的时间进行了抽样调查，并将调查结果绘制成下列两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
（1）这次抽样共调查了名学生，并补全条形统计图；
（2）计算扇形统计图中表示户外活动时间0.5小时的扇形圆心角度数；
（3）本次调查学生参加户外活动的平均时间是否符合要求？（写出判断过程）
（本题6分）一艘中国海监船自西向东航行，在A处测得钓鱼岛C在海监船的北偏东68°方向，继续向东航行80海里到达B处，此时测得钓鱼岛C在海监船的北偏东26°方向上．问：海监船再继续向东航行多少海里，距离钓鱼岛C最近？（结果保留整数）（参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.48，sin26°≈0.44，cos26°≈0.90，tan26°≈0.49）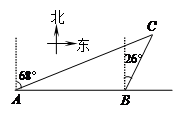
（本题6分） 如图，已知点B，E，C，D在同一直线上，AB=FD，∠B=∠D，请你添加一个条件，使AC=FE，并给出证明(不再添加其它线段，不再标注或使用其他字母).
你添加的条件是:；
证明:
（本题12分）如图1，已知在直角坐标系XOY中，正△OBC的边长和等腰直角△DEF的底边都为6，点E与坐标原点O重合，点D、B在X轴上，连结FC，在△DEF沿X轴的正方向以每秒
个单位运动时，边EF所在直线和边OC所在直线相交于G，设运动时间为t.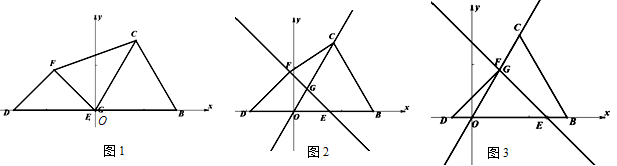
（1）如图2，当t=1时，①求OE的长；②求∠FGC的度数；③求G点坐标；
（2）①如图3，当t为多少时，点F恰在△OBC的OC边上；
②在点F、C、G三点不共线时，记△FCG的面积为S，用含t的代数式表示S，并写出t的相应取值范围.