(本小题共13分)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是 ,且面试是否合格互不影响.
,且面试是否合格互不影响.
(Ⅰ)求至少有1人面试合格的概率;
(Ⅱ)求签约人数 的分布列和数学期望
的分布列和数学期望
甲乙两个野生动物保护区有相同的自然环境,且野生动物种类和数量也大致相等,而两个保护区每个季度发现违反保护条例的事件次数的分布如下:
甲乙
| X |
0 |
1 |
2 |
3 |
| P |
0.3 |
0.3 |
0.2 |
0.2 |
| X |
0 |
1 |
2 |
| P |
0.1 |
0.5 |
0.4 |
试评定这两个保护区的管理水平.
设事件A发生的概率为p(0<p<1),
(1)证明事件A在一次试验中发生次数ε的方差不超过 .
.
(2) 求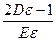 的最大值
的最大值
(3)在n次独立重复实验中,事件A发生次数ξ的方差最大值是多少?
将一枚硬币抛掷n次,求正面次数与反面次数之差ξ的概率分布,并求出ξ的期望Eξ与方差Dξ.
某次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题,并宣
布:观众答对问题A可获奖金2a元;答对问题B可获奖金3a元,答对两题则可获5a元.先答哪个问题由观众选择,只有第1题答对才能答第2题,否则中止答题.若你被选为幸运观众,且假设你答对A、B的概率分别为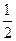 、
、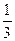 ,你觉得应先回答哪个问题?说明理由.
,你觉得应先回答哪个问题?说明理由.
A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3。按以往多次比赛的统计,对阵队员之间胜负概率如下:
| 对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
| A1对B1 |
2 3 |
1 3 |
| A2对B2 |
2 5 |
3 5 |
| A3对B3 |
2 5 |
3 5 |
现按表中对阵方式出场, 每场胜队得1分, 负队得0分,设A队、B队最后总分分别为x、h.
(Ⅰ) 求x、h的概率分布;
(Ⅱ) 求Ex、Eh.