(本小题满分13分)甲班有2名男乒乓球选手和3名女乒乓球选手,乙班有3名男乒乓球选手和1名女乒乓球选手,学校计划从甲乙两班各选2名选手参加体育交流活动.
(Ⅰ)求选出的4名选手均为男选手的概率.
(Ⅱ)记 为选出的4名选手中女选手的人数,求
为选出的4名选手中女选手的人数,求 的分布列和期望.
的分布列和期望.
椭圆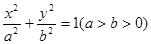 与
与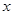 轴负半轴交于点
轴负半轴交于点 ,
,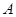 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线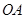 交椭圆于另一点
交椭圆于另一点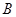 ,椭圆左焦点为
,椭圆左焦点为 ,连接
,连接 交
交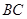 于点D。
于点D。
(1)如果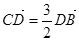 ,求椭圆的离心率;
,求椭圆的离心率;
(2)在(1)的条件下,若直线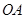 的倾斜角为
的倾斜角为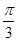 且△ABC的面积为
且△ABC的面积为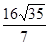 ,求椭圆的标准方程。
,求椭圆的标准方程。
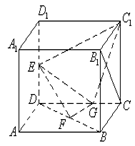
已知在正方体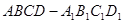 中
中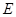 ,
,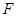 分别是
分别是 的中点,
的中点,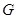 在棱
在棱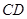 上,且
上,且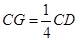 .
.
(1)求证: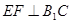 ; (2)求二面角
; (2)求二面角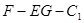 的大小.
的大小.
在一段时间内,某种商品价格 (万元)和需求量
(万元)和需求量 之间的一组数据为:
之间的一组数据为:
价格 |
1.4 |
1.6 |
1.8 |
2 |
2.2 |
需求量 |
12 |
10 |
7 |
5 |
3 |
(1)进行相关性检验;
(2)如果 与
与 之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01
之间具有线性相关关系,求出回归直线方程,并预测当价格定为1.9万元,需求量大约是多少?(精确到0.01 )
)
参考公式及数据: ,
, ,
,
相关性检验的临界值表:
| n-2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 小概率0.01 |
1.000 |
0.990 |
0.959 |
0.917 |
0.874 |
0.834 |
0.798 |
0.765 |
0.735 |
0.708 |
在△ABC中, ,记
,记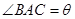 ,△ABC的面积为
,△ABC的面积为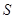 ,且满足
,且满足 .
.
(1)求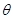 的取值范围;
的取值范围;
(2)求函数 的最大值和最小值.
的最大值和最小值.
已知函数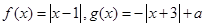

(I) 解关于 的不等式
的不等式  ;
;
(II)若函数 的图象恒在函数
的图象恒在函数 的上方,求实数
的上方,求实数 的取值范围。
的取值范围。