(本小题满分14分)已知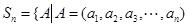 ,
, 或1,
或1,
 ,对于
,对于 ,
,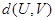 表示U和V中对应位置的元素不同的个数.
表示U和V中对应位置的元素不同的个数.
(Ⅰ)令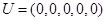 ,求所有满足
,求所有满足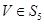 ,且
,且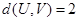 的
的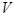 的个数;
的个数;
(Ⅱ)令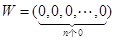 ,若
,若 ,求证:
,求证: ;
;
(Ⅲ)给定 ,
, ,若
,若 ,求所有
,求所有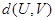 之和.
之和.
在△ 中,三个内角
中,三个内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,
, =(b,
=(b, a),
a), =(cosB,sinA),且
=(cosB,sinA),且 ||
|| (Ⅰ)求角
(Ⅰ)求角 ;(Ⅱ)若
;(Ⅱ)若 ,c=2a, 求△
,c=2a, 求△ 的面积.
的面积.
用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
| 年级 |
相关人数 |
抽取人数 |
| 高一 |
99 |
 |
| 高二 |
27 |
 |
| 高三 |
18 |
2 |
(Ⅰ)求 ,
, ;
;
(Ⅱ)若从高二、高三年级抽取的人中选 人,求这二人都来自高二年级的概率.
人,求这二人都来自高二年级的概率.
已知 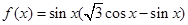
(Ⅰ)求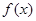 的单调增区间;(Ⅱ)当
的单调增区间;(Ⅱ)当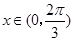 时,求
时,求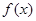 的取值范围.
的取值范围.
已知等比数列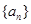 的各项均为正数,
的各项均为正数, ,
, .
.
(Ⅰ)求数列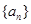 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设 .证明:
.证明: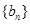 为等差数列,并求
为等差数列,并求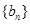 的前
的前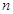 项和
项和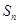 .
.
设数列{an} 的前n项和为Sn,满足2Sn=an+1﹣2n+1+1,n∈N*,且a1,a2+5,a3成等差数列.
(1)求a1,a2,a3的值;
(2)求证:数列{an+2n}是等比数列;
(3)证明:对一切正整数n,有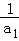 +
+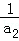 +…+
+…+ <
< .
.