阅读下列材料，并解决相关的问题．
按照一定顺序排列着的一列数称为数列，排在第一位的数称为第1项，记为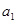
，依次类推，排在第
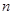位的数称为第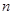项，记为
．
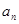一般地，如果一个数列从第二项起，每一项与它前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母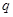
表示（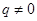
）．如：数列1，3，9，27，…为等比数列，其中
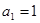，公比为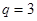
．
则：（1）等比数列3，6，12，…的公比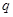为，第4项是．
（2）如果一个数列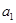
，
，
，
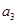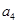，…是等比数列，且公比为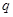，那么根据定义可得到：
，
，
，…… 
．
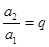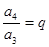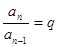所以：
，
，
，
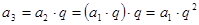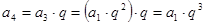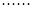
由此可得：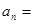
（用
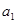和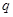的代数式表示）
（3）若一等比数列的公比q=2，第2项是10，请求它的第1项与第4项．
如图1是“东方之星”救援打捞现场图，小红据此构造出一个如图2所示的数学模型，已知：A．B、D三点在同一水平线上，CD⊥AD，∠A=30°，∠CBD=75°，AB=60m．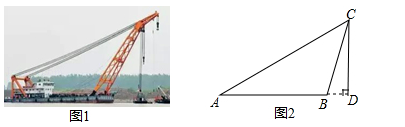
（1）求点B到AC的距离；
（2）求线段CD的长度．
小华从家里到学校的路是一段平路和一段下坡路，假设他始终保持平路每分钟走60m，下坡路每分钟走80m，上坡路每分钟走40m，则他从家里到学校需10min，从学校到家里需15min．问：从小华家到学校的平路和下坡路各有多远？
先化简，再求值：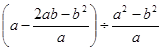
，其中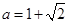
，
．
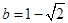如图，在边长均为1的正方形网格纸上有一个△ABC，顶点A、B、C及点O均在格点上，请按要求完成以下操作或运算：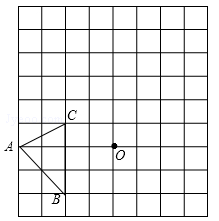
（1）将△ABC向上平移4个单位，得到△A1B1C1（不写作法，但要标出字母）；
（2）将△ABC绕点O旋转180°，得到△A2B2C2（不写作法，但要标出字母）；
（3）求点A绕着点O旋转到点A2所经过的路径长．
，其中x是方程x2-2x=0的根．