如图,已知:AD∥BC,AD=CB,AE=CF,
(1)请问∠B=∠D吗?为什么?
(2)不改变其他条件,提出一个你认为正确的结论,并说明理由?
在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.
八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
| 甲 |
7 |
8 |
9 |
7 |
10 |
10 |
9 |
10 |
10 |
10 |
| 乙 |
10 |
8 |
7 |
9 |
8 |
10 |
10 |
9 |
10 |
9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是_____分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.
(1)先化简,再求值:(a+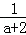 )÷(a﹣2+
)÷(a﹣2+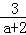 ),其中a=2
),其中a=2
(2)解分式方程: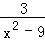 +
+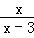 =1.
=1.
[问题提出]
学习了三角形全等的判定方法(即“SAS”,“ASA”,“AAS”,“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
[初步思考]我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
[深入探究]
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据________,可以知道Rt△ABC≌Rt△DEF.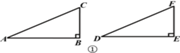
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角.求证:△ABC≌△DEF.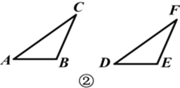
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹).
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接填写结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,若________,则△ABC≌△DEF.
如图,A、B、C三点在同一直线上,分别以AB、BC为边,在直线AC的同侧作等边△ABD和等边△BCE,连接AE交BD于点M,连接CD交BE于点N,连接MN得△BMN.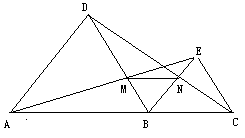
(1)求证:△ABE≌△DBC.
(2)试判断△BMN的形状,并说明理由.