如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC等于多少米?
已知:如图,在四边形ABCD中,AB∥CD,∠A=90°,CD=6,AB=15, .
.
求:BC的长.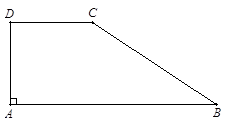
已知二次函数y1=ax2+bx-3的图象经过点A(2,-3),B(-1,0),与y轴交于点C,与x轴另一交点交于点D.
(1)求二次函数的解析式;
(2)求点C、点D的坐标;
(3)若一条直线y2,经过C、D两点,请直接写出y1>y2时, 的取值范围.
的取值范围.
如图,已知直线 与反比例函数
与反比例函数 的图象相交于点A(-1,a),并且与x轴相交于点B.
的图象相交于点A(-1,a),并且与x轴相交于点B.
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积.
已知:如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E.
(1)求证:∠CDB=∠A;
(2)若BD=5,AD=12,求CD的长.