（1）已知一元二次方程x2-4x+m=0有唯一实数根，求
的值；
（2）小明是这样完成“作∠MON的平分线”这项作业的：
“如图，①以O为圆心，任意长为半径画弧，分别交OM，ON于点A，B；②分别作线段OA，OB的垂直平分线l1，l2（垂足分别记为C，D），记l1与l2的交点为P；③作射线OP，则射线OP为∠MON的平分线．”
你认为小明的作法正确吗？如果正确，请你给证明，如果不正确，请指出错在哪里．
已知：如图，B、F、C、D在同一条直线上，∠ACB=∠EFD，BF=CD，AC=EF．求证：AB∥ED．
如图1，直线y=﹣
x+2
分别与x轴、y轴交于点M，N．Rt△ABC的顶点B与原点O重合，BC在x轴正半轴上，BC=1，∠ABC=60°．将△ABC沿x轴正方向以每秒1个单位长度的速度平移，当点B与点M重合时，△ABC停止运动，设运动时间为t秒．
（1）当点A落在直线MN上时，求t的值；
（2）在（1）基础上，△ABC继续平移，AB，AC分别交线段MN于点E，F（如图2）．
①t为何值时，S△AEF=
S△ABC；
②若当点A刚好落在直线MN上时，动点P同时从顶点B出发，以每秒个单位长度的速度沿B→A运动，△ABC停止平移时，点P随之停止．则在点P运动的过程中，是否存在某一时刻，△PEF与△MON相似？若存在，求出此时t的值；若不存在，请说明理由．
基本模型
如图1，点A，F，B在同一直线上，若∠A=∠B=∠EFC=90°，易得△AFE∽△BCF．
（1）模型拓展：
如图2，点A，F，B在同一直线上，若∠A=∠B=∠EFC，求证：△AFE∽△BCF；
（2）拓展应用：如图3，AB是半圆⊙O的直径，弦长AC=BC=4
，E，F分别是AC，AB上的一点，若∠CFE=45°．若设AE=y，BF=x，求出y与x的函数关系式及y的最大值；
（3）拓展提升：如图4，在平面直角坐标系柳中，抛物线y=﹣
（x+4）（x﹣6）与x轴交于点A，C，与y轴交于点B，抛物线的对称轴交线段BC于点E，探求线段AB上是否存在点F，使得∠EFO=∠BAO？若存在，求出BF的长；若不存在，请说明理由．
为更好地响应丽水市的创国卫活动，某校抽取了2015届九年级部分同学对饮食卫生知识进行了测试，并将测试结果按照A，B，C，D四个等级绘制成如下两个统计图，请结合图中信息解答下列问题：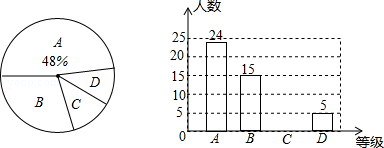
（1）请把条形统计图补充完整，并求出扇形统计图中B部分所对应的圆心角的度数；
（2）该校共有学生1 000人，若把测试结果为A的记为优秀，请根据样本估计全校饮食卫生知识了解情况达到优秀的学生人数是多少？
（3）为进一步提高学生对饮食卫生知识的知晓率，学校又连续组织了两次测试，最后一次达到优秀的学生增加到750人，求平均每次的增长率．
如图，以AB为直径的⊙O经过AC的中点D，DE⊥BC于点E．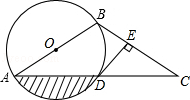
（1）求证：DE是⊙O的切线；
（2）当DE=1，∠C=30°时，求图中阴影部分的面积．