如图1,直线y=﹣ x+2
x+2 分别与x轴、y轴交于点M,N.Rt△ABC的顶点B与原点O重合,BC在x轴正半轴上,BC=1,∠ABC=60°.将△ABC沿x轴正方向以每秒1个单位长度的速度平移,当点B与点M重合时,△ABC停止运动,设运动时间为t秒.
分别与x轴、y轴交于点M,N.Rt△ABC的顶点B与原点O重合,BC在x轴正半轴上,BC=1,∠ABC=60°.将△ABC沿x轴正方向以每秒1个单位长度的速度平移,当点B与点M重合时,△ABC停止运动,设运动时间为t秒.
(1)当点A落在直线MN上时,求t的值;
(2)在(1)基础上,△ABC继续平移,AB,AC分别交线段MN于点E,F(如图2).
①t为何值时,S△AEF= S△ABC;
S△ABC;
②若当点A刚好落在直线MN上时,动点P同时从顶点B出发,以每秒 个单位长度的速度沿B→A运动,△ABC停止平移时,点P随之停止.则在点P运动的过程中,是否存在某一时刻,△PEF与△MON相似?若存在,求出此时t的值;若不存在,请说明理由.
个单位长度的速度沿B→A运动,△ABC停止平移时,点P随之停止.则在点P运动的过程中,是否存在某一时刻,△PEF与△MON相似?若存在,求出此时t的值;若不存在,请说明理由.
(广安)如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若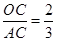 ,且OC=4,求PA的长和tanD的值.
,且OC=4,求PA的长和tanD的值.
(广安)如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l: 经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线
经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线 顶点E在直线l上.
顶点E在直线l上.
(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;
(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;
(3)设抛物线与y轴交于G点,当抛物线顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.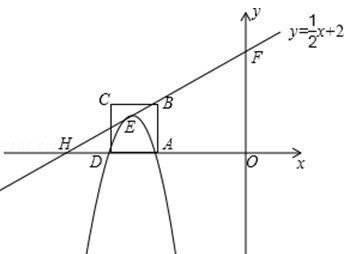
(广元)经统计分析.某市跨河大桥上的车流速度v(千米/时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞.此时车流速度为0千米/时;当车流密度不超过20辆/千米,车流速度为80千米/时.研究表明:当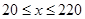 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在某一交通时段.为使大桥上的车流速度大于60千米/时且小于80千米/时,应把大桥上的车流密度控制在什么范围内?
(广元)如图,AB是⊙O的弦,D为半径OA的中点.过D作CD⊥OA交弦AB于点E,交⊙O于点F.且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA= .求⊙O的半径.
.求⊙O的半径.
(广元)如图,已知抛物线 (
( )与x轴相交干点A、B.与y轴相交于点C,且点A在点B的左侧.
)与x轴相交干点A、B.与y轴相交于点C,且点A在点B的左侧.
(1)若抛物经过点C(2,2),求实数m的值;
(2)在(1)的条件下,解答下列问题:
①求出△ABC的面积;
②在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,使得以点A、B、M为顶点的三角形与△ACB相似?若存在,求m的值;若不存在.请说明理由.