为更好地响应丽水市的创国卫活动，某校抽取了2015届九年级部分同学对饮食卫生知识进行了测试，并将测试结果按照A，B，C，D四个等级绘制成如下两个统计图，请结合图中信息解答下列问题：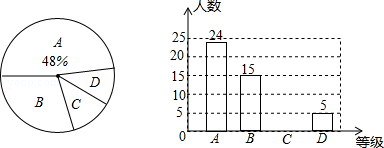
（1）请把条形统计图补充完整，并求出扇形统计图中B部分所对应的圆心角的度数；
（2）该校共有学生1 000人，若把测试结果为A的记为优秀，请根据样本估计全校饮食卫生知识了解情况达到优秀的学生人数是多少？
（3）为进一步提高学生对饮食卫生知识的知晓率，学校又连续组织了两次测试，最后一次达到优秀的学生增加到750人，求平均每次的增长率．
如图1，在正方形ABCD中，点E、F分别在边BC、CD上，且BE=DF，点P是AF的中点，点Q是直线AC与EF的交点，连接PQ、PD．
（1）求证：AC垂直平分EF；
（2）试判断△PDQ的形状，并加以证明；
（3）如图2，若将△CEF绕着点C旋转180°，其余条件不变，则（2）中的结论还成立吗？若成立，请加以证明；若不成立，请说明理由．
如图，直线y=
x+2与x轴交于点A，与y轴交于点B，动点P从点A开始沿折线AB﹣BO以1cm/s的速度运动到点O．设点P运动的时间为t（s），△PAO面积为S（cm2）．（坐标轴的单位长度为cm）
（1）当点P在线段AB上运动到与点O距离最小时，求S的值；
（2）在整个运动过程中，求S与t之间的函数表达式；
（3）当点P运动几秒后，△PAO面积为2cm2？
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CAB=2∠CBF．
（1）试判断：直线BF与⊙O的位置关系，并说明理由；
（2）若AB=6，BF=8，求tan∠CBF．
一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10．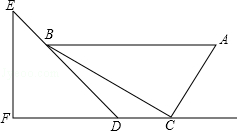
（1）求直线AB与CF之间的距离；
（2）求CD的长．
甲、乙两个袋中均装有三张除标数值外完全相同的卡片，甲袋中的三张卡片上所标的数值为﹣7，﹣1，3，乙袋中的三张卡片所标的数值为﹣2，1，6，先从甲袋中随机取出一张卡片，用x表示取出的卡片上的数值，再从乙袋中随机取出一张卡片，用y表示取出卡片上的数值，把x、y分别作为点A的横坐标和纵坐标．
（1）用列表或画树形图的方法写出点A（x，y）的所有的情况；
（2）在题（1）的所有点中随机抽取一点，试求出该点落在直线y=2x上的概率．