选修4—4:坐标系与参数方程
极坐标系与直角坐标系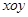 有相同的长度单位,以原点为极点,以
有相同的长度单位,以原点为极点,以 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线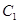 的极坐标方程为
的极坐标方程为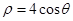 ,曲线
,曲线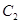 的参数方程为
的参数方程为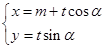 (
(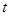 为参数,
为参数,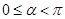 ),射线
),射线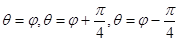 与曲线
与曲线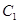 交于(不包括极点O)三点
交于(不包括极点O)三点
(1)求证: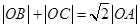 ;
;
(2)当 时,B,C两点在曲线
时,B,C两点在曲线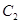 上,求
上,求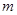 与
与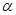 的值
的值
(本大题满分14分)
设函数 上两点
上两点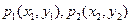 ,若
,若 ,且P点的横坐标为
,且P点的横坐标为 .
.
(1)求P点的纵坐 标;
标;
(2)若 求
求 ;
;
(3)记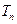 为数列
为数列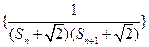 的前n项和,若
的前n项和,若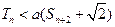 对一切
对一切 都成立,试求a的取值范围.
都成立,试求a的取值范围.
(本大题满分13分)
已知函数 在
在 处取得极值
处取得极值
(1)求b与a的关系;
(2)设函数 ,如果
,如果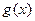 在区间(
在区间( 0,1)上存在极小值,求实数a的取值范围
0,1)上存在极小值,求实数a的取值范围
(本大题满分12分)
某公司预计全年分批购入每台价值为2 000元的电视机共3600台,每批都购入x台
000元的电视机共3600台,每批都购入x台 ,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰
,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰 当安排每批进货的数量,使资金够用?写出你的结论并说明理由
当安排每批进货的数量,使资金够用?写出你的结论并说明理由
(本大题满分12分)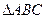 中角A的对边长等于2,向量
中角A的对边长等于2,向量 向量
向量 .
.
(1)当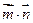 取最大值时,求角A的大小;
取最大值时,求角A的大小;
(2)在(1)条件下,求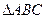 面积的最大值.
面积的最大值.
(本大题满分12分)
平面内有向量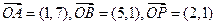 ,点X为直线OP上的一动点。
,点X为直线OP上的一动点。
(1)当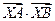 取最小值时,求
取最小值时,求 的坐标;
的坐标;
(2)当点X满足(1)的条件和结论时,求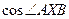 的值.
的值.