(本小题满分12分)已知函数 .
.
(I)讨论函数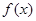 的单调区间;
的单调区间;
(II)当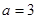 时,若函数
时,若函数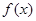 在区间
在区间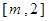 上的最大值为
上的最大值为 ,求
,求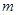 的取值范围.
的取值范围.
(本小题满分14分)已知函数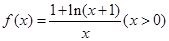 .
.
(Ⅰ)函数 在区间
在区间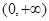 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;
(Ⅱ)当 时,
时,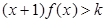 恒成立,求整数
恒成立,求整数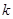 的最大值;
的最大值;
(Ⅲ)试证明: (
(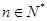 )。
)。
(本小题满分13分)已知椭圆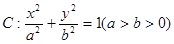 的两焦点在
的两焦点在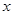 轴上, 且两焦点与短轴的一个顶点的连线构成斜边长为2的等腰直角三角形。
轴上, 且两焦点与短轴的一个顶点的连线构成斜边长为2的等腰直角三角形。
(Ⅰ)求椭圆的方程;
(Ⅱ)过点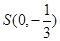 的动直线
的动直线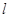 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点Q,使得以AB为直径的圆恒过点Q ?若存在求出点Q的坐标;若不存在,请说明理由。
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点Q,使得以AB为直径的圆恒过点Q ?若存在求出点Q的坐标;若不存在,请说明理由。
(本小题满分12分)如图1,在Rt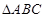 中,
中,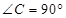 ,
,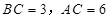 .D、E分别是
.D、E分别是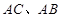 上的点,且
上的点,且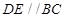 ,将
,将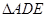 沿
沿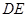 折起到
折起到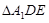 的位置,使
的位置,使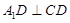 ,如图2.
,如图2.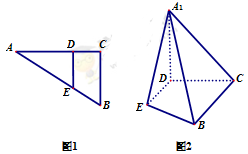
(Ⅰ)求证:平面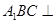 平面
平面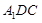 ;
;
(Ⅱ)若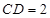 ,求
,求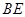 与平面
与平面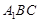 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当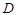 点在何处时,
点在何处时,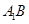 的长度最小,并求出最小值.
的长度最小,并求出最小值.
(本小题满分12分)在数列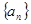 中,
中,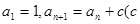 为常数,
为常数,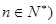 ,且
,且 成公比不等于1的等比数列.
成公比不等于1的等比数列.
(Ⅰ)求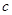 的值;
的值;
(Ⅱ)设 ,求数列
,求数列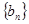 的前
的前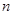 项和
项和 。
。
(本小题满分12分)若盒中装有同一型号的灯泡共10只,其中有8只合格品,2只次品。
(Ⅰ)某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;
(Ⅱ)某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数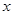 的分布列和数学期望。
的分布列和数学期望。