(本小题满分10分 )选修4—4:坐标系与参数方程
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,圆
轴的正半轴为极轴的极坐标系下,圆 的方程为
的方程为 .
.
(Ⅰ)求直线 的普通方程和圆
的普通方程和圆 的圆心的极坐标;
的圆心的极坐标;
(Ⅱ)设直线 和圆
和圆 的交点为
的交点为 、
、 ,求弦
,求弦 的长.
的长.
直四棱柱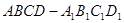 的底面
的底面 是菱形,
是菱形,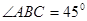 ,其侧面展开图是边长为
,其侧面展开图是边长为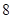 的正方形。
的正方形。 、
、 分别是侧棱
分别是侧棱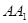 、
、 上的动点,
上的动点, .
.
(I)证明: ;
;
(II)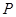 在棱
在棱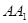 上,且
上,且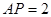 ,若
,若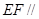 平面
平面 ,求
,求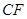 .
.
某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 |
初二年级 |
初三年级 |
|
| 女生 |
373 |
 |
 |
| 男生 |
377 |
370 |
 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19。
(I)求 的值;
的值;
(II)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(III)已知 ,求初三年级中女生比男生多的概率。
,求初三年级中女生比男生多的概率。
设函数
(I)写出函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(II)当 时,函数
时,函数 的最大值与最小值的和为
的最大值与最小值的和为 ,解不等式
,解不等式 .
.
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,右焦点到直线x+y+1=0的距离为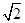 .
.
(1)求椭圆的方程;
(2)直线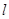 过点P(0,2)且与椭圆相交于A,B的点,当△AOB面积取得最大值时,求直线
过点P(0,2)且与椭圆相交于A,B的点,当△AOB面积取得最大值时,求直线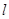 的方程.
的方程.
如图,正四棱柱 中,底面边长为2,侧棱长为3,E为BC的中点,F、G分别为
中,底面边长为2,侧棱长为3,E为BC的中点,F、G分别为 、
、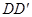 上的点,且CF=2GD=2.求:
上的点,且CF=2GD=2.求:
(1)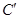 到面EFG的距离;
到面EFG的距离;
(2)DA与面EFG所成的角的正弦值;
(3)在直线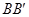 上是否存在点P,使得DP//面EFG?,若存在,找出点P的位置,若不存在,试说明理由。
上是否存在点P,使得DP//面EFG?,若存在,找出点P的位置,若不存在,试说明理由。