为了研究过山车的原理，某兴趣小组提出了下列设想：取一个与水平方向夹角为37°、长为l = 2.0m的粗糙倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除 AB 段以外都是光滑的。其AB 与BC 轨道以微小圆弧相接，如图所示．一个小物块以初速度
＝4.0m/s从某一高处水平抛出，到A点时速度方向恰好沿 AB 方向，并沿倾斜轨道滑下．已知物块与倾斜轨道的动摩擦因数 μ = 0.50．（g＝10 m／s2、sin37°＝ 0.60、cos37° ＝0.80）
（1）求小物块到达A点时速度。
（2）要使小物块不离开轨道，并从轨道DE滑出，求竖直圆弧轨道的半径应该满足什么条件？
（3）为了让小物块不离开轨道，并且能够滑回倾斜轨道 AB，则竖直圆轨道的半径应该满足什么条件？
已知地球半径为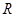
=6400km，地面上重力加速度
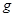="9.80" m/s2，万有引力常量
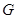=6.67×10-11N·m2/kg2，如不考虑地球自转影响，求地球的平均密度表达式及大小。（大小结果保留两位有效数字）
有两滑块AB置于光滑的水平面上，A的质量为m，B的质量为2m，在水平面的右侧有一粗糙的斜面，斜面很长且倾角为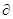
，A、B两物体与斜面的动摩擦因素均为
，且最大的静摩擦力等于滑动摩擦力。现突然给A施一水平向右冲量I，A、B碰撞无机械能损失，滑块由水平面运动至斜面也不考虑转弯处的机械能损失。求
1．A受冲量作用后的速度大小？
2．求AB碰后的速度?
3．若AB只发生一次碰撞，求摩擦力对B做功?
某同学为了探究涡流制动原理，在玩具小车的底部固定了一个水平放置的矩形线圈abcd，小车（含线圈）总质量为4kg，闭合线圈共100匝，线圈长Lab=Lcd=20cm,线圈宽Lbc=Lad=10cm，线圈的电阻为0.5欧，在小车轨道的正前方布置了一个固定的磁场区，磁场的边界始终与线圈bc边平行，磁场的方向竖直向下，磁感应强度B=0.2T，忽略小车与轨道面的摩擦，小车的初速度为2m/s。当线圈刚进入磁场时，求
1线圈中感应电流的大小？
2线圈受安培力的大小？
3小车加速度大小？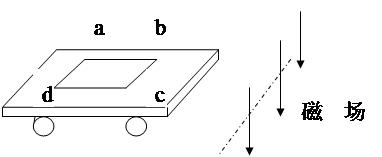
如图所示，在y<0的区域内存在匀强磁场，磁场方向垂直于xy平面并指向纸面外，磁感应强度为B，一带正电的粒子以速度v0从O点射入磁场，入射方向在xy平面内，与x轴正向夹角为θ=π/6，若粒子射出磁场的位置与O点的距离为L，试求：（要求必须画出示意图）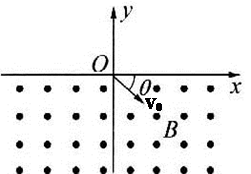
（1）该粒子的电量和质量之比为多少?
（2）该粒子在匀强磁场中运动的时间？
如图中电源电动势E＝10 V，内阻可忽略，R1＝R2＝5 Ω，C＝30 μF，求：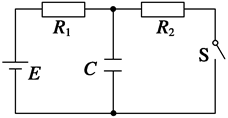
(1)S闭合稳定后通过R1的电流；
(2)S原来闭合，然后断开，求这个过程中流过R1的总电荷量。