（本小题满分12分）
已知定点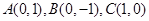
，动点
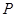满足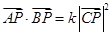
。
（1）求动点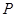的轨迹方程，并说明方程表示的曲线；
（2）当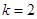
时，求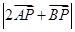
的最大值和最小值。
已知方程x2＋y2－2(m＋3)x＋2(1－4m2)y＋16m4＋9＝0表示一个圆．
(1)求实数m的取值范围；(2)求该圆半径r的取值范围；(3)求圆心的轨迹方程．
已知集合A=
B=
（1）当m=3时，求A
(
RB)；
（2）若AB 
，求实数m的值.
（本小题满分15分）已知直线l的方程为：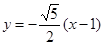
，直线l与x轴的交点为F， 圆O的方程为：
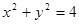，C、 D在圆上， CF⊥DF，设线段CD的中点为M．
（1）如果CFDG为平行四边形，求动点G的轨迹；
（2）已知椭圆的中心在原点，右焦点为F，直线l交椭圆于A、B两点，又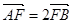
，
求椭圆C的方程．
（本小题满分15分）
函数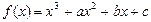
，曲线
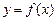上点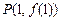
处的切线方程为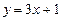
（1）若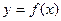
在
时有极值，求函数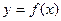在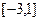
上的最大值；
（2）若函数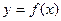在区间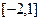
上单调递增，求
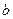的取值范围．
（本小题满分14分）
数列{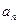
}满足递推式
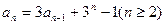，其中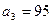
．
（1）求a1，a2；
（2）是否存在一个实数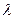
，使得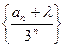
为等差数列，如果存在，求出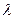的值；如果不存在，试
说明理由；
（3）求数列{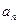}的前n项之和．