某商场的销售部经过市场调查发现，该商场的某种商品每日的销售量
（单位：千克）与销售价格
（单位：元/千克）满足关系式
，其中
，
为常数，已知销售价格为
元/千克时，每日可售出该商品
千克．
（Ⅰ）求的值；
（Ⅱ）若该商品的成本为
元/千克，试确定销售价格的值，使该商场每日销售该商品所获得的利润最大.
已知圆x2＋y2＋2ax－2ay＋2a2－4a＝0(0＜a≤4)的圆心为C，直线l：y＝x＋m.
(1)若m＝4，求直线l被圆C所截得弦长的最大值；
(2)若直线l是圆心下方的切线，当a在的变化时，求m的取值范围．
已知圆x2＋y2－4ax＋2ay＋20(a－1)＝0.
(1)求证对任意实数a，该圆恒过一定点；
(2)若该圆与圆x2＋y2＝4相切，求a的值
设O为坐标原点，曲线x2＋y2＋2x－6y＋1＝0上有两点P、Q，满足关于直线x＋my＋4＝0对称，又满足·＝0.
(1)求m的值；
(2)求直线PQ的方程．
求过两点A(1,4)、B(3,2)，且圆心在直线y＝0上的圆的标准方程．并判断点M1(2,3)，M2(2,4)与圆的位置关系．
在平面直角坐标系中，已知矩形ABCD的长为2，宽为1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合如右图所示．将矩形折叠，使A点落在线段DC上．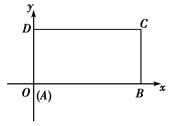
若折痕所在直线的斜率为k，试写出折痕所在直线的方程．