已知 与
与 成正比例,且
成正比例,且 时,
时, .
.
(1)求 与
与 的函数关系式;
的函数关系式;
(2)当 时,求
时,求 的值;
的值;
(3)将所得函数图象平移,使它过点(2, -1).求平移后直线的解析式.
正比例函数 y=kx 和一次函数 y=ax+b的图象都经过点 A(1,2),且一次函数的图象交 x 轴于点 B(4,0).求正比例函数和一次函数的表达式.
如图,抛物线C1:y=ax2+bx+1的顶点坐标为D(1,0),求抛物线C1的解析式;
如图1,将抛物线C1向右平移1个单位,向下平移1个单位得到抛物线C2,直线y=x+c,经过点D交y轴于点A,交抛物线C2于点B,抛物线C2的顶点为P,求△DBP的面积
如图2,连接AP,过点B作BC⊥AP于C,设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,试证明:FC·(AC+EC)为定值.

如图,矩形ABCD中,AB=4,AD=5,将矩形ABCD绕点A顺时针旋转,得到矩形AMNP,直线MN分别与边BC、CD交于点E、F.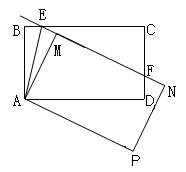
判断BE与ME的数量关系,并加以证明;
当△CEF是等腰三角形时,求线段BE的长;
设x=BE,y=CF·(AB2-BE2),试求y与x之间的函数关系式,并求出y的最大值.
阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数, a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.填空:i3=_____,i4="_______" ;
计算:①
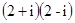 ;②
;②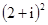 ;
;若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.试一试:请利用以前学习的有关知识将
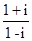 化简成a+bi的形式
化简成a+bi的形式