一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同.进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x如图2所示.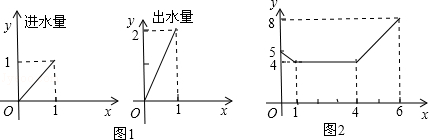
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
阅读下列材料:
正方形网格中,每个小正方形的顶点称为格点.以格点为顶点的多边形叫格点多边形,若格点多边形至少有一边是曲线,则称其为曲边格点多边形.
(1)求图(1)中格点三角形的面积;
(2)在图(2)中画出一个格点梯形,使它的面积等于9;(只需画出,不必说明)
(3)在图(3)中画出一个曲边格点多边形,使它的面积等于25,说明理由.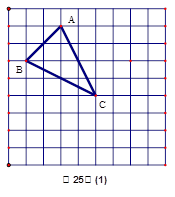
.已知函数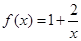 ,其中
,其中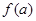 表示当
表示当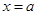 时对应的函数值,即
时对应的函数值,即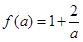 .
.
(1)求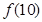 ;
;
(2)计算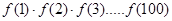 的值;
的值;
(3)如果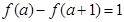 ,试求
,试求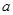 的值.
的值.
已知⊙O的半径为 ,该平面上另有一点P,⊙P的半径为
,该平面上另有一点P,⊙P的半径为 .请讨论⊙O与⊙P的位置关系.
.请讨论⊙O与⊙P的位置关系.
张华调查了一个报亭某一天A、B、C三种报纸的销售量,并把调查结果绘制成如下条形统计图.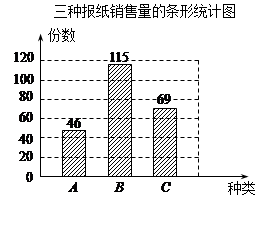
(1)求该天A、C报纸的销售量各占这三种报纸销售量之和的百分比;
(2)请绘制该天A、B、C三种报纸销售量的扇形统计图;
(3)如果报亭准备按上述比例购进A、B、C三种报纸共100份,应该购进这三种报纸各多少份?
已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形?并说明理由.