如图,将矩形OABC置于平面直角坐标系xOy中,A(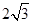 ,0),C(0,2).
,0),C(0,2).
(1)抛物线y=-x2+bx+c经过点B、C,求该抛物线的解析式;
(2)将矩形OABC绕原点顺时针旋转一个角度α(0°<α<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标;
(3)如图(2),将矩形OABC绕原点顺时针旋转一个角度θ(0°<θ<180°),将得到矩形OA′B′C′,设A′C′的中点为点E,连接CE,当θ= 时,线段CE的长度最大,最大值为 .
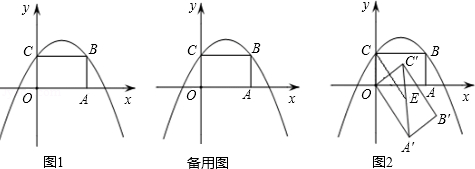
由于受甲型H1N1流感(起初叫猪流感)的影响,4月初某地猪肉价格大幅度下跌,下跌后每斤猪肉价格是原价格的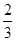 ,原来用60元买到的猪肉下跌后可多买2斤.4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上升为每斤14.4元.
,原来用60元买到的猪肉下跌后可多买2斤.4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上升为每斤14.4元.
(1)求4月初猪肉价格下跌后每斤多少元.
(2)求5、6月份猪肉价格的月平均增长率.
如图,在四边形ABCD中,AC平分∠DAB,CE⊥AB于E.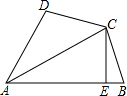
(1)若AB=AD+2BE,求证:BC=DC;
(2)若∠B=60°,AC=7,AD=6,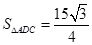 ,求AB的长.
,求AB的长.
A箱中有三张质地相同的卡片,它们分别写有数字-1,-2,3,B箱中装有三张质地相同的卡片,它们分别写有数字1,-1,2.现从A箱,B箱中,各随机地取出一张卡片,请你用画树状图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率;
(2)两张卡片上的数字之积为正数的概率.
如图所示, A 、 B 两地之间有条河,原来从 A 地到 B 地需要经过桥 DC ,沿折线 A → D → C → B 到达.现在新建了桥 EF ,可直接沿直线 AB 从 A 地到达 B 地.已知 BC ="11" km ,∠ A =45°,∠ B =37°,桥 DC 和 AB 平行,则现在从 A 地到 B 地可比原来少走多少路程 (结果精确到0.1 km ,参考数据:  )
) 
已知 ,且
,且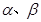 为锐角,求
为锐角,求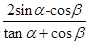 的值 。
的值 。