(本小题满分12分)
某工厂投资生产A产品时,每生产一百吨需要资金200万元,需要场地200平方米,可获利润300万元;投资生产B产品时,每生产一百吨需要资金300万元,需要场地100平方米,可获利润200万元。现在该工厂可使用资金1400元,场地900平方米,问应做怎样的组合投资,可使获利最大?并求出最大利润(以百万元为单位)。
(本小题满分12分)
如图所示,在海拔为500m的海岛A处,测得海面上两船C、D的俯角分别为45°和30°,又测得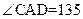 °,求C、D两船间的距离。
°,求C、D两船间的距离。
(本大题满分12分)
已知数列 ,
, 的通项公式分别为
的通项公式分别为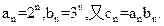
(I)求证数列{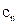 }是等比数列;
}是等比数列;
(II)求数列{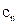 }的前n项和为
}的前n项和为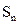 。
。
(本大题满分10分)
已知 的顶点坐标分别为A(-1,1),B(2,7),C(-4,5)。
的顶点坐标分别为A(-1,1),B(2,7),C(-4,5)。
求AB边上的高CD所在的直线方程。
(本小题满分14分)
已知圆C过点P(1,1)且与圆M: 关于直线
关于直线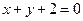 对称
对称
(1)求圆C的方程
(2)设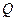 为圆C上一个动点,求
为圆C上一个动点,求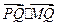 的最小值
的最小值
(3)过点P作两条相异直线分别与圆C相交于A、B两点,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP与AB是否平行,并请说明理由.