某汽车制造厂开发了一款新式电动汽车,计划一年生产安装360辆,由于抽调不出足够的熟练工人来完成新式电动汽车的安装,工厂决定招聘一些新工人,他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:3名熟练工和2名新工人每月可安装24辆电动汽车;2名熟练工和3名新工人每月可安装21辆电动汽车.
(1)每名熟练工和每人新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发3000元的工资,给每名新工人每月发1800元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时支出的工资总额w(元)尽可能少?
解方程:
(1)
(2)
已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)点A表示的数为,点B表示的数为,点C表示的数为.
(2)用含t的代数式表示P到点A和点C的距离: PA= ,PC=.
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动, Q点到达C点后,再立即以同样的速度返回,运动到终点A.
①在点Q向点C运动过程中,能否追上点P?若能,请求出点Q运动几秒追上.
②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.

商场销售某种冰箱,该种冰箱每台进价为2500元,已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
| 每天的销售量/台 |
每台销售利润/元 |
|
| 降价前 |
8 |
400 |
| 降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
如图,点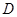 在
在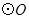 的直径
的直径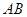 的延长线上,点
的延长线上,点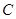 在
在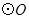 上,
上,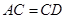 ,
,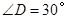
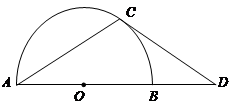
(1)求证:CD是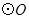 的切线;
的切线;
(2)若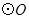 的半径为3,求CD的长.
的半径为3,求CD的长.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.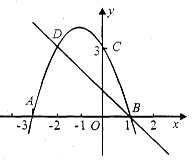
(1)D点坐标(,);
(2)求一次函数的表达式;
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.