如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8)。动点M、N分别从O、B同时出发,以每秒1个单位的速度运动。其中,点M沿OA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥BC,交AC于P,连结MP。已知动点运动了x秒。
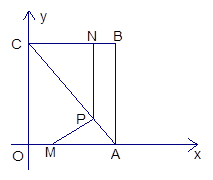
(1)P点的坐标为( , );(用含x的代数式表示)
(2)试求 ⊿MPA面积的最大值,并求此时x的值。
(3)请你探索:当x为何值时,⊿MPA是一个等腰三角形?
你发现了几种情况?写出你的研究成果。
为积极响应市委政府“加快建设天蓝•水碧•地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
已知抛物线 的图象与y轴交于点 ,顶点为B.
(1)试确定a的值,并写出B点的坐标;
(2)若一次函数的图象经过A、B两点,试写出一次函数的解析式;
(3)试在x轴上求一点P,使得△PAB的周长取最小值;
(4)若将抛物线平移 个单位,所得新抛物线的顶点记作C,与原抛物线的交点记作D,问:点O、C、D能否在同一条直线上?若能,请求出m的值;若不能,请说明理由.
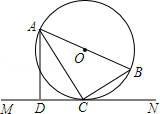
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且 .
(1)求证:直线MN是⊙O的切线;
(2)若 , ,求⊙O的半径.
张家界到长沙的距离约为320km,小明开着大货车,小华开着小轿车,都从张家界同时去长沙,已知小轿车的速度是大货车的1.25倍,小华比小明提前1小时到达长沙.试问:大货车和小轿车的速度各是多少?
如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度 ,求旗杆AB的高度(结果精确到0.1米).参考数据: .
