水平放置的两根平行金属导轨ad和bc，导轨两端a、b和c、d两点分别连接电阻R1和R2，组成矩形线框，如图所示，ad和bc相距L＝0.5 m，放在竖直向下的匀强磁场中，磁感应强度为B＝1 T，一根电阻为0.2 Ω的导体棒PQ跨接在两根金属导轨上，在外力作用下以4 m/s的速度，向右匀速运动，如果电阻R1＝0.3 Ω，R2＝0.6 Ω，导轨ad和bc的电阻不计，导体与导轨接触良好．求：
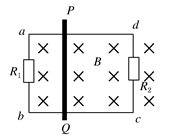
(1)导体棒PQ中产生的感应电流的大小；
(2)导体棒PQ上感应电流的方向；
(3)导体棒PQ向右匀速滑动的过程中，外力做功的功率．
如图所示，空间有一垂直纸面的磁感应强度为0.5T的匀强磁场，一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上，在木板左端无初速放置一质量为0.1kg、电荷量q=+0.2C的滑块，滑块与绝缘木板之间动摩擦因数为0.5，滑块受到的最大静摩擦力可认为等于滑动摩擦力。t=0时对木板施加方向水平向左，大小为0.6N恒力，g取10m/s2。则（）
| A．木板和滑块一直做加速度为2m/s2的匀加速运动 |
| B．滑块开始做加速度减小的变加速运动，最后做速度为10m/s匀速运动 |
| C．木板先做加速度为2m/s2匀加速运动，再做加速度增大的运动，最后做加速度为3m/s2的匀加速运动 |
| D．t=5s后滑块和木块有相对运动 |
为了研究过山车的原理，某兴趣小组提出了下列设想：取一个与水平方向夹角为37°、长为l = 2.0m的粗糙倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除 AB 段以外都是光滑的。其AB 与BC 轨道以微小圆弧相接，如图所示．一个小物块以初速度
＝4.0m/s从某一高处水平抛出，到A点时速度方向恰好沿 AB 方向，并沿倾斜轨道滑下．已知物块与倾斜轨道的动摩擦因数 μ = 0.50．（g＝10 m／s2、sin37°＝ 0.60、cos37° ＝0.80）
（1）求小物块到达A点时速度。
（2）要使小物块不离开轨道，并从轨道DE滑出，求竖直圆弧轨道的半径应该满足什么条件？
（3）为了让小物块不离开轨道，并且能够滑回倾斜轨道 AB，则竖直圆轨道的半径应该满足什么条件？
如图所示，让质量m=5.0kg的摆球由图中所示位置A从静止开始下摆，摆至最低点B点时恰好绳被拉断。已知摆线长L=1.6m，悬点O与地面的距离OC=4.0m。若空气阻力不计，摆线被拉断瞬间小球的机械能无损失。(g取10 m/s2)求：
（1）摆线所能承受的最大拉力T；
（2）摆球落地时的动能。
如图所示，质量为m的物体放在水平桌面上，在与水平方向成θ角的恒力F作用下加速向右运功，已知物体与桌面间的动摩擦因数为μ，求：
（1）物体所受的摩擦力；
（2）物体的加速度．
一辆汽车以72km/h的速度行驶，现因故紧急刹车并最终停止运动．已知汽车刹车过程加速度的大小为5m/s2，则从开始刹车经过5s，汽车的位移是多大？