在平面直角坐标系上,第二象限角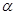 的终边与单位圆交于点
的终边与单位圆交于点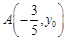 .
.
(1)求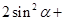
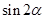 的值;
的值;
(2)若向量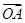 与
与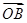 夹角为
夹角为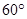 ,且
,且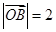 ,求直线
,求直线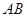 的斜率.
的斜率.
已知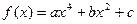 的图象经过点
的图象经过点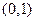 ,且在
,且在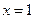 处的切线方程是
处的切线方程是
求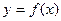 的解析式;
的解析式;
有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)共有多少种放法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒不放球,有多少种放法?
(本小题满分14分)
已知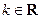 函数
函数 .
.
(I) 若 且函数
且函数 为奇函数,求实数
为奇函数,求实数 ;
;
(II) 若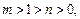 试判断函数
试判断函数 的单调性;
的单调性;
(III) 当 ,
, ,
, 时,求函数
时,求函数 的对称轴或对称中心.
的对称轴或对称中心.
(本小题满分12分)
设椭圆 :
: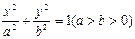 的焦点分别为
的焦点分别为 、
、 ,抛物线
,抛物线 :
: 的准线与
的准线与 轴的交点为
轴的交点为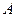 ,且
,且 .
.
(I)求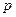 的值及椭圆
的值及椭圆 的方程;
的方程;
(II)过 、
、 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于 、
、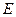 、
、 、
、 四点(如图),
四点(如图),
求四边形 面积的最大值和最小值.
面积的最大值和最小值.
本小题满分12分)
已知数列 满足
满足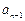 +
+ =4n-3(n∈
=4n-3(n∈ ).
).
(I)若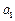 =2,求数列
=2,求数列 的前n项和
的前n项和 ;
;
(II)若对任意n∈ ,都有
,都有 ≥5成立,求
≥5成立,求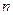 为偶数时,
为偶数时,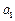 的取值范围.
的取值范围.