(本小题满分16分)对于函数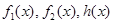 ,如果存在实数
,如果存在实数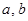 使得
使得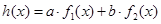 ,那么称
,那么称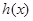 为
为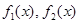 的生成函数.
的生成函数.
(1)下面给出两组函数,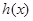 是否分别为
是否分别为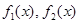 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: ;
;
第二组: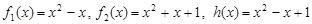 ;
;
(2)设 ,生成函数
,生成函数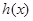 .若不等式
.若不等式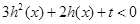 在
在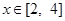 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
设椭圆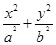 =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为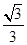 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为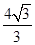 .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若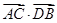 +
+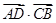 =8,求k的值.
=8,求k的值.
已知椭圆C的中心为平面直角坐标系xOy的原点,焦点在x轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆C的方程;
(2)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的一点,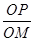 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.
设F1,F2分别是椭圆E:x2+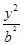 =1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
=1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
(1)求|AB|;
(2)若直线l的斜率为1,求b的值.
已知以点C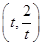 (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.