(本小题满分13分)甲、乙二人用4张扑克牌(分别是红心2、红心3、红心4、方块4)
玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,
各抽一张.
(Ⅰ)写出甲、乙二人抽到的牌的所有基本事件; (Ⅱ)当甲抽到红心3时,求乙抽出的牌的牌面数字比3大的概率;
(Ⅱ)当甲抽到红心3时,求乙抽出的牌的牌面数字比3大的概率;
(Ⅲ)甲、乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜;反之,则乙胜,你认为
此游戏是否公平说明你的理由.
设椭圆 :
: ,直线
,直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重合,
轴重合, 与椭圆交于
与椭圆交于 ,当
,当 与
与 轴垂直时,
轴垂直时,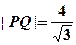 ,
, 为椭圆的右焦点,
为椭圆的右焦点, 为椭圆
为椭圆 上任意一点,若
上任意一点,若 面积的最大值为
面积的最大值为 。
。
(1)求椭圆 的方程;
的方程;
(2)直线 绕着
绕着 旋转,与圆
旋转,与圆 :
: 交于
交于 两点,若
两点,若 ,求
,求 的面积
的面积 的取值范围。
的取值范围。
如图一,平面四边形ABCD关于直线AC对称, ,
, ,
, 。
。
把 沿BD折起(如图二),使二面角A-BD-C的余弦值等于
沿BD折起(如图二),使二面角A-BD-C的余弦值等于 。对于图二,
。对于图二,
(1)求 的长,并证明:
的长,并证明: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值。
所成角的正弦值。
数列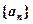 的前
的前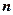 项和为
项和为 ,
, ,
,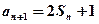 ,等差数列
,等差数列 满足
满足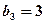 ,
,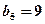 。
。
(1)分别求数列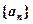 ,
, 的通项公式;
的通项公式;
(2)若对任意的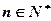 ,
, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
在 中,角
中,角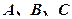 所对的边分别为
所对的边分别为 ,且满足
,且满足 。
。
(1)求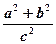 的值;
的值;
(2)若点 在双曲线
在双曲线 上,求
上,求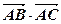 的值
的值
(本小题满分14分)
已知函数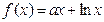
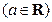 .
.
(Ⅰ)若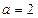 ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得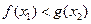 ,求
,求 的取值范围.
的取值范围.