已知 中∠ACB=90°,SA⊥面ABC,AD⊥SC于D,
中∠ACB=90°,SA⊥面ABC,AD⊥SC于D,
求证: AD⊥面SBC;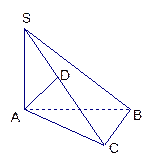
已知向量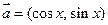 ,
,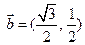 ,函数
,函数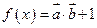 。
。
(Ⅰ)求函数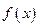 的值域;
的值域;
(Ⅱ)当 ,且
,且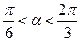 时,求
时,求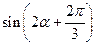 的值
的值
已知过点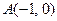 的动直线
的动直线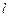 与圆
与圆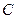 :
: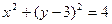 相交于
相交于 、
、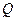 两点,
两点,  与
与
直线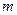 :
: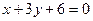 相交于
相交于 .
.
(1)求证:当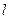 与
与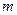 垂直时,
垂直时,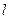 必过圆心
必过圆心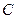 ;
;
(2)当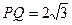 时,求直线
时,求直线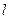 的方程.
的方程.
已知中心在原点、焦点在x轴的椭圆的离心率为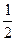 ,且过点(
,且过点(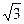 ,
, ).
).
(Ⅰ)求椭圆E的方程;
(Ⅱ)若A,B是椭圆E的左、右顶点,直线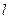 :
: (
(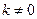 )与椭圆E交于
)与椭圆E交于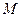 、
、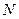 两点,证明直线
两点,证明直线 与直线
与直线 的交点在垂直于
的交点在垂直于 轴的定直线上,并求出该直线方程.
轴的定直线上,并求出该直线方程.
等差数列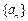 中,
中,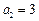 ,
, ;数列
;数列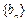 的前
的前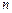 项和是
项和是 ,且
,且 .
.
(Ⅰ) 求数列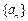 的通项公式;
的通项公式;
(Ⅱ) 求证:数列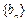 是等比数列;
是等比数列;
(Ⅲ) 记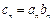 ,求
,求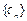 的前n项和
的前n项和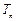 .
.