如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90，AC=BC，OA=1，OC=4，抛物线y=x2+bx+c经过A，B两点，抛物线的顶点为D．
（1）求b，c的值；
（2）点E是直角三角形ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；
（3）在（2）的条件下：
①求以点E、B、F、D为顶点的四边形的面积；
②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，说明理由．
（·黑龙江牡丹江）甲、乙两车从A地出发沿同一路线驶向B地，甲车先出发匀速驶向B地．40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B地．甲乙两车距A地的路程y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示．
请结合图象信息解答下列问题：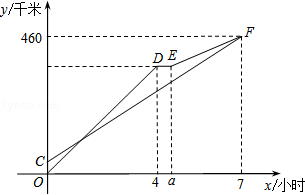
（1）直接写出a的值，并求甲车的速度；
（2）求图中线段EF所表示的y与x的函数关系式，并直接写出自变量x的取值范围；
（3）乙车出发多少小时与甲车相距15千米？直接写出答案．
（·黑龙江牡丹江）如图，抛物线y=x2+bx+c经过点A（﹣1，0），B（3，0）．请解答下列问题：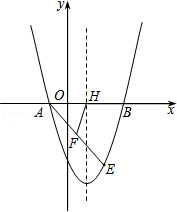
（1）求抛物线的解析式；
（2）点E（2，m）在抛物线上，抛物线的对称轴与x轴交于点H，点F是AE中点，连接FH，求线段FH的长．
注：抛物线y=ax2+bx+c（a≠0）的对称轴是x=﹣
．
（·黑龙江大庆）如图，一次函数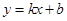
的图象与反比例函数
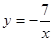的图象交于A（﹣1，m）、B（n，﹣1）两点．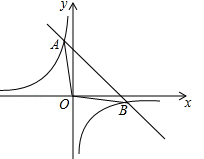
（1）求一次函数的解析式；
（2）求△AOB的面积．
（·辽宁盘锦）盘锦红海滩景区门票价格80元/人，景区为吸引游客，对门票价格进行动态管理，非节假日打a折，节假日期间，10人以下（包括10人）不打折，10人以上超过10人的部分打b折，设游客为x人，门票费用为y元，非节假日门票费用
（元）及节假日门票费用
（元）与游客x（人）之间的函数关系如图所示．
（1）a= ，b= ；
（2）直接写出、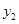与x之间的函数关系式；
（3）导游小王6月10日（非节假日）带A旅游团，6月20日（端午节）带B旅游团到红海滩景区旅游，两团共计50人，两次共付门票费用3040元，求A、B两个旅游团各多少人？
（·辽宁朝阳）某农场急需铵肥8吨，在该农场南北方向分别有一家化肥公司A、B，A公司有铵肥3吨，每吨售价750元；B公司有铵肥7吨，每吨售价700元，汽车每千米的运输费用b（单位：元/千米）与运输重量a（单位：吨）的关系如图所示．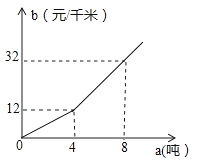
（1）根据图象求出b关于a的函数解析式（包括自变量的取值范围）；
（2）若农场到B公司的路程是农场到A公司路程的2倍，农场到A公司的路程为m千米，设农场从A公司购买x吨铵肥，购买8吨铵肥的总费用为y元（总费用=购买铵肥费用+运输费用），求出y关于x的函数解析式（m为常数），并向农场建议总费用最低的购买方案．