(本小题满分16分)已知各项均为正数的等差数列{an}的公差d不等于0,设a1、a3、ak是公比为q的等比数列{bn}的前三项.
(1)若k=7,a1=2.
①求数列{anbn}的前n项和Tn;
②将数列{an}与{bn}中相同的项去掉,剩下的项依次构成新的数列{cn},设其前n项和为Sn,求S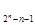 -22n-1+3·2n-1的值;
-22n-1+3·2n-1的值;
(2)若存在m>k,m∈N*使得a1、a3、ak、am成等比数列,求证:k为奇数.
已知函数 .
.
(1)求 的值域和最小正周期;
的值域和最小正周期;
(2)若对任意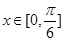 ,使得
,使得 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知椭圆 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设不过原点 的直线
的直线 与椭圆
与椭圆 交于两点
交于两点 、
、 ,且直线
,且直线 、
、 、
、 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△ 面积的取值范围.
面积的取值范围.
已知 .
.
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)若存在 ,使不等式
,使不等式 成立,求
成立,求 的取值范围.
的取值范围.
我市某校某数学老师这学期分别用 两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的数学期末考试成绩,分别为
两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的数学期末考试成绩,分别为
甲班: .
.
乙班: .
.
(Ⅰ)作出甲乙两班分别抽取的20名学生数学期末成绩的茎叶图,依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班所抽数学成绩不低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
如图,正三棱柱 中,
中, 是
是 的中点,
的中点, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求点 到平面
到平面 的距离.
的距离.