选修41:几何证明选讲
如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.

(1)求证:OM·OP=OA2;
(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.求证:∠OKM=90°.
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合如右图所示.将矩形折叠,使A点落在线段DC上.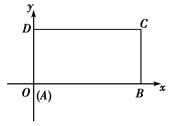
若折痕所在直线的斜率为k,试写出折痕所在直线的方程.
已知△ABC的一个顶点A(-1,-4),∠B、∠C的平分线所在直线的方程分别为l1:y+1=0,l2:x+y+1=0,求边BC所在直线的方程.
已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0,求一点P使|PA|=|PB|,且点P到l的距离等于2.
对任意的实数λ,直线(2+λ)x-(1+λ)y-2(3+2λ)=0与点P(-2,2)的距离为d,求d的取值范围
已知直线l:kx-y+1+2k=0