(本小题满分12分)某项选拔共有三轮考核,每轮设有一个问题,回答问题正确者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三轮的问题的概率分别为 ,
, ,
, ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(1)求该选手被淘汰的概率;
(2)记该选手在考核中回答问题的个数为 ,求随机变量
,求随机变量 的分布列与数学期望.
的分布列与数学期望.
设函数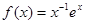 的定义域为(0,
的定义域为(0, ).
).
(Ⅰ)求函数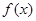 在
在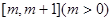 上的最小值;
上的最小值;
(Ⅱ)设函数 ,如果
,如果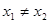 ,且
,且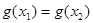 ,证明:
,证明: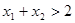 .
.
如图,椭圆 经过点
经过点 离心率
离心率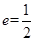 ,直线
,直线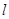 的方程为
的方程为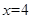 .
.
(Ⅰ)求椭圆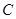 的方程;
的方程;
(Ⅱ) 是经过右焦点
是经过右焦点 的任一弦(不经过点
的任一弦(不经过点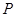 ),设直线
),设直线 与直线
与直线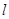 相交于点
相交于点 ,记
,记 的斜率分别为
的斜率分别为 问:是否存在常数
问:是否存在常数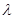 ,使得
,使得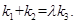 若存在求
若存在求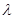 的值;若不存在,说明理由.
的值;若不存在,说明理由.
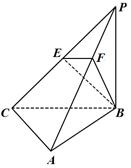
如图,三棱锥 中,
中,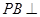 底面
底面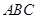 ,
, ,
, ,
, 为
为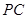 的中点,点
的中点,点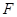 在
在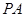 上,且
上,且 .
.
(Ⅰ)求证:平面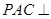 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面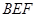 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.
一个袋子里装有7个球, 其中有红球4个, 编号分别为1,2,3,4; 白球3个, 编号分别为2,3,4. 从袋子中任取4个球 (假设取到任何一个球的可能性相同).
(Ⅰ) 求取出的4个球中, 含有编号为3的球的概率;
(Ⅱ) 在取出的4个球中, 红球编号的最大值设为X ,求随机变量X的分布列和数学期望.
在△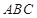 中,内角
中,内角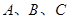 的对边分别为
的对边分别为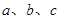 ,已知
,已知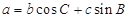 .
.
(Ⅰ)求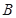 ;
;
(Ⅱ)若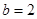 ,求△
,求△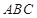 面积的最大值.
面积的最大值.