(本小题满分14分)已知函数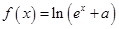 (
( 为常数,
为常数, 为自然对数的底数)是实数集
为自然对数的底数)是实数集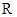 上的奇函数,函数
上的奇函数,函数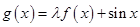 在区间
在区间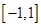 上是减函数.
上是减函数.
(1)求实数 的值;
的值;
(2)若 在
在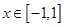 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 的根的个数.
的根的个数.
某教育机构为了研究人具有大学专科以上学历(包括大学专科)和对待教育改革态度的关系,随机抽取了392名成年人进行调查,所得数据如下表所示:
| 积极支持教育改革 |
不太赞成教育改革 |
合计 |
|
| 大学专科以上学历 |
39 |
157 |
196 |
| 大学专科以下学历 |
29 |
167 |
196 |
| 合计 |
68 |
324 |
392 |
对于教育机构的研究项目,根据上述数据能得出什么结论.
某公司“咨询热线”电话共有8路外线,经长期统计发现,在8点到10点这段时间内,外线电话同时打入情况如下表所示:
| 电话同时 打入个数  |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
概率 |
0.13 |
0.35 |
0.27 |
0.14 |
0.08 |
0.02 |
0.01 |
0 |
0 |
(1)若这段时间内,公司只安排了2位接线员(一个接线员一次只能接一个电话)
①求至少一路电话不能一次接通的概率;
②在一周五个工作日中,如果有三个工作日的这段时间(8点至10点)内至少一路电话不能一次接通,那么公司的形象将受到损害,现用至少一路电话不能一次接通的概率表示公司形象的“损害度”,求上述情况下公司形象的“损害度”.
(2)求一周五个工作日的这段时间(8点至10点)内,电话同时打入数X的均值.
在函数 ,
, 的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数
的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数 与曲线形状的关系,并运用指数函数的有关性质加以说明.
与曲线形状的关系,并运用指数函数的有关性质加以说明.
一批产品分一、二、三级,其中一级品的数量是二级品的两倍,三级品的数量是二级品的一半,从这批产品中随机抽取一个检查其品级,用随机变量描述检验的可能结果,写出它的分布列.
张华同学上学途中必须经过 四个交通岗,其中在
四个交通岗,其中在 岗遇到红灯的概率均为
岗遇到红灯的概率均为 ,在
,在 岗遇到红灯的概率均为
岗遇到红灯的概率均为 .假设他在4个交通岗遇到红灯的事件是相互独立的,X表示他遇到红灯的次数.
.假设他在4个交通岗遇到红灯的事件是相互独立的,X表示他遇到红灯的次数.
(1)若 ,就会迟到,求张华不迟到的概率;(2)求EX.
,就会迟到,求张华不迟到的概率;(2)求EX.