如图，已知，在Rt△ABC中，∠BAC=90°．
实践与操作：
（1）①利用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）：作线段AC的垂直平分线MN，垂足为O；
②连接BO，并延长BO到点D，使得OD=BO，连接AD、CD；
③分别在OA、OC的延长线上取点E、F，使AE=CF，连接BF、FD、DE、EB．
推理与运用：
（2）①求证：四边形BFDE是平行四边形；
②若AB=4，AC=6，求当AE的长为多少时，四边形BFDE是矩形．
我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售．按计划，20辆汽车都要装运，每辆汽车只能装运同一种脐橙，且必须装满．根据下表提供的信息，解答以下问题：
（1）设装运A种脐橙的车辆数为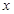
，装运B种脐橙的车辆数为
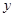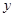，求与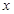之间的函数关系式；
（2）如果装运每种脐橙的车辆数都不少于4辆，那么车辆的安排方案有几种？并写出每种安排方案；
（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值．
如图，已知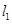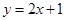直线
：
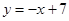、直线
：
，直线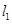、分别交x轴于B、C两点，、相交于点A．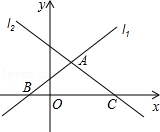
（1）求A、B、C三点坐标；
（2）求△ABC的面积．
如图，△ABC三个顶点的坐标分别为A（2，3）、B（1，1）、C（5，1），先将△ABC作关于x轴的轴对称图形得到△A1B1C1，再将△A1B1C1向左平移5个单位得△A2B2C2．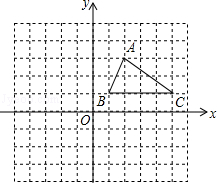
（1）分别画出两次变换的像△A1B1C1与△A2B2C2；
（2）求出边AB所在直线的函数解析式，并判断点C2是否在该直线上．
AC，BD相交于点O，AO=OC，再添加一个什么条件，使两个三角形全等？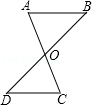
解不等式组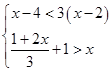
，并在数轴上表示解集．