如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
(本题满分10分)先化简,再求值: ,其中
,其中 .
.
计算: .
.
某检修小组乘汽车检修公路道路。向东记为正,向西记为负。某天自A地出发。所走路程(单位:千米)为:+22,-3,+4,-2,-8,-17,-2,+12,+7,-5;
问:(1)最后他们是否回到出发点?若没有,则在A地的什么地方?距离A地多远?
(2)若每千米耗油0.05升,则今天共耗油多少升?
将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
探索规律:用棋子按下面的方式摆出正方形
(1)按图示规律填写下表:
| 图形编号 |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| 棋子个数 |
(2)按照这种方式摆下去,摆第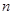 个正方形需要多少个棋子?
个正方形需要多少个棋子?
(3)按照这种方式摆下去,摆第 个正方形需要多少个棋子?
个正方形需要多少个棋子?