某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，根据这组数据绘制成如图所示的统计图．
（1）这一组学生平均每人捐款多少元？
（2）这组数据的众数是20 ，中位数是14.5 ；
（3）请估计该校2000名学生中捐款为20元的人数．
已知：如图，△ABC中，AD⊥BC于点D，AD=DC，∠FCD=∠BAD，点F在AD上，BF的延长线交AC于点E．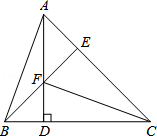
（1）求证：△ABD≌△CFD．
（2）求证：BE⊥AC；
（3）设CE的长为m，用含m的代数式表示AC+BF．
如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC．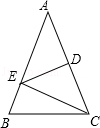
（1）求∠ECD的度数；
（2）若CE=5，求BC长．
解分式方程：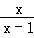
﹣
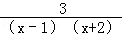=1．
如图，在△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥GF，交AB于点E，连接EG．
（1）求证：BG=CF；
（2）请你判断BE+CF与EF的大小关系，并证明你的结论．
(5分)先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式x2﹣4＞0
解：∵x2﹣4=（x+2）（x﹣2）
∴x2﹣4＞0可化为
（x+2）（x﹣2）＞0
由有理数的乘法法则“两数相乘，同号得正”，得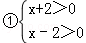
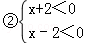
解不等式组①，得x＞2，
解不等式组②，得x＜﹣2，
∴（x+2）（x﹣2）＞0的解集为x＞2或x＜﹣2，
即一元二次不等式x2﹣4＞0的解集为x＞2或x＜﹣2．
（1）一元二次不等式x2﹣16＞0的解集为x＞4或x＜﹣4；
（2）分式不等式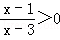
的解集为x＞3或x＜1 ；
（3）解一元二次不等式2x2﹣3x＜0．