育人中学开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种
活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生
进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
(1)样本中最喜欢A项目的人数所占的百分比为________ ,其所在扇形统计图中对应的
圆心角度数是 ______度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
如图,E、F是线段BD上的两点,且DF=BE,AE=CF,AE∥CF.求证:AD∥BC.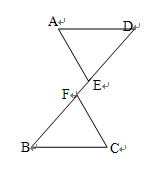
①计算: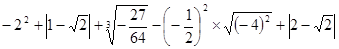
②已知: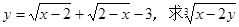 的平方根.
的平方根.
如图,直线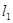 交直线
交直线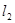 于
于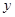 轴上一点
轴上一点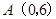 ,交
,交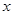 轴上另一点
轴上另一点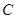 ,
,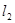 交
交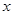 轴于另一点
轴于另一点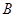 ,二次函数
,二次函数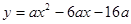 (
(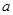 >0)的图像过点
>0)的图像过点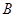 、
、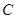 两点,点
两点,点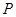 是线段
是线段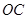 上由
上由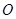 向
向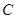 移动的动点,线段
移动的动点,线段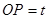 (1<
(1<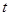 <8)。
<8)。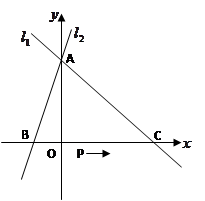
⑴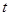 为何值时,
为何值时,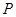 为圆心
为圆心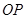 为半径的圆与
为半径的圆与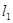 相切;
相切;
⑵设抛物线对称轴与直线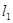 相交于点
相交于点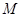 ,请在
,请在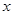 轴上求一点
轴上求一点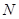 ,使
,使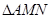 的周长最小;
的周长最小;
⑶设点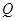 是
是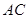 上由
上由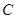 向
向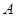 移动的一动点,且
移动的一动点,且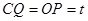 ,若
,若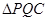 的面积为
的面积为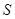 ,求
,求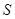 与
与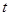 的函数关系式,当
的函数关系式,当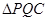 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出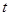 的值。
的值。
如图,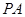 为⊙O的切线,
为⊙O的切线,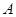 为切点,连接
为切点,连接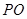 并延长,与圆相交于点
并延长,与圆相交于点 ,
,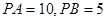 ,∠
,∠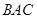 的平分线与
的平分线与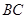 和⊙O分别相交于点
和⊙O分别相交于点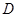 和
和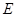 。
。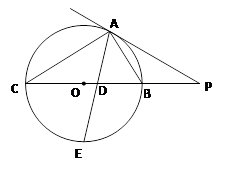
求:⑴⊙O的半径;⑵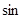 ∠
∠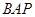 的值;⑶
的值;⑶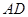 ·
· 的值。
的值。
已知,关于的 方程
方程 (
( 为整数)的根为整数,双曲线
为整数)的根为整数,双曲线
 >0
>0 过梯形
过梯形 的顶点
的顶点 和腰
和腰 中点
中点 ,如图所示,且∠
,如图所示,且∠ ,求四边形
,求四边形 的面积。
的面积。