已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若曲线C1的方程为ρ2=8ρsinθ﹣15,曲线 C2的方程为 (
( 为参数).
为参数).
(1)将C1的方程化为直角坐标方程;
(2)若C2上的点Q对应的参数为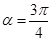 ,P为C1上的动点,求PQ的最小值.
,P为C1上的动点,求PQ的最小值.
已知函数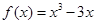
(1)求函数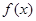 在
在 上的最大值和最小值
上的最大值和最小值
(2)过点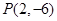 作曲线
作曲线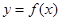 的切线,求此切线的方程
的切线,求此切线的方程
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(Ⅰ)记“函数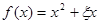 为R上的偶函数”为事件A,求事件A的概率;
为R上的偶函数”为事件A,求事件A的概率;
(Ⅱ)求 的分布列和数学期望.
的分布列和数学期望.
已知()n展开式中的倒数第三项的系数为45,求:
(1)含x3的项;
(2)系数最大的项.
已知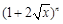 的展开式中,某一项的系数是它前一项系数的2倍,而等于它后一项的系数的
的展开式中,某一项的系数是它前一项系数的2倍,而等于它后一项的系数的 .
.
(1)求该展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
|
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB = 60°的菱形,AC BD = O,A1C1
BD = O,A1C1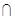 B1D1 = O1,E是O1A的中点.
B1D1 = O1,E是O1A的中点.