(本小题满分14分)已知函数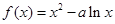 ,曲线
,曲线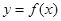 在点
在点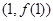 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求函数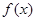 的最小值;
的最小值;
(Ⅱ)当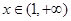 时,
时,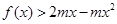 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知椭圆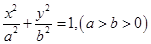 的离心率为
的离心率为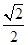 ,且过点
,且过点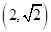

(1)求椭圆的标准方程:
(2)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,若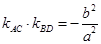
①求 的最值:
的最值:
②求证:四边形ABCD的面积为定值.
.已知圆 :x2+y2-2x-2y-2=0.
:x2+y2-2x-2y-2=0.
(1)若直线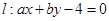 平分圆
平分圆 的周长,求原点O到直线
的周长,求原点O到直线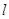 的距离的最大值;
的距离的最大值;
(2)若圆 平分圆
平分圆 的周长,圆心
的周长,圆心 在直线y=2x上,求符合条件且半径最小的圆B的方程.
在直线y=2x上,求符合条件且半径最小的圆B的方程.
如图,将边长为2,有一个锐角为60°的菱形 ,沿着较短的对角线
,沿着较短的对角线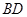 对折,使得
对折,使得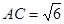 ,
,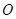 为
为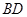 的中点.若P为AC上的点,且满足
的中点.若P为AC上的点,且满足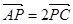 。
。
(Ⅰ)求证: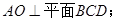
(Ⅱ)求三棱锥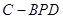 的体积;
的体积;
(Ⅲ)求二面角 的余弦值.
的余弦值.
平面内动点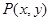 到定点
到定点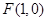 的距离比它到
的距离比它到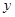 轴的距离大
轴的距离大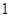 。
。
(1)求动点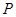 的轨迹
的轨迹 的方程;
的方程;
(2)已知点A(3,2), 求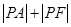 的最小值及此时P点的坐标.
的最小值及此时P点的坐标.
某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组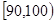 ,第二组
,第二组 ,,第五组
,,第五组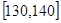 .按上述分组方法得到的频率分布直方图如图所示.
.按上述分组方法得到的频率分布直方图如图所示.
(1)若成绩大于或等于100分且小于120分认为是良好的,求该校参赛学生在这次数学联赛中成绩良好的人数;
(2)若从第一、五组中共随机取出两个成绩,求这两个成绩差的绝对值大于30分的概率.